Ferromagnetic QCP in Heavy-fermions
Y. Komijani, P. Coleman, Model for Ferromagnetic Quantum Critical Point in a 1D Kondo Lattice, Phys. Rev. Lett. 120, 157206 (2018).
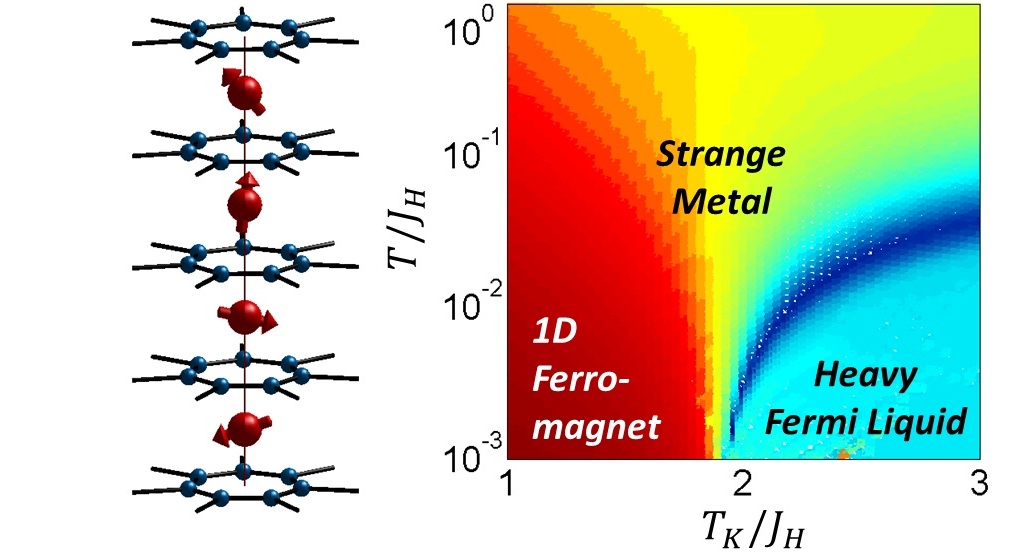
- beta-YbAlB4 is a heavy-fermion that is myteriously quantum critical over a wide range of pressure around ambient pressure. It is composed of weakly coupled quasi-1D chains of Yb magnetic moments that are sadnwitched between B layers. The neutron scattering experiments indicate that Yb moments are ferromagnetically correalted along the chain.
- We used a large-N Schwinger-Boson representation of spins and a multi-channel Kondo descrpition of the Kondo screening to study Kondo-Heisenberg model that appear in this model, wihtin the so-called independent screening approxmation.
- We showed that as the Doniach parameter TK/JH is tuned, the Kondo temperature is suppressed to zero temperature at a quantum critical point (QCP) that separates FL from a 1D ferromagnetic phaase Each chain thus acts as a macroscopic moment, which is coupled to other chains via a frustrated antiferromagentic coupling.
- This is a fascinating system and I am still investigating various generalizations.
Ferromagnetic QCP in CeRh6Ge4
B. Shen, Y. Zhang, Y. Komijani, M. Nicklas, ..., M. Smidman, F. Steglich, P. Coleman, H. Yuan Strange metal behavior in a pure ferromagnetic Kondo lattice, ArXiv:1907.10470.

- CeRh6Ge4 is a heavy-fermion ferromagnet with very little disorder. Upon application of hydrostatic pressure, the Curie tempersture can be reduced to zero, transitioning into a Fermi liquid. At the QCP, the material exhibits strange metal behavior: linear-in-Temperature resistivity and logarithmic-in-Temperature specific heat coefficient, similar to Cuprates (figure).
- This was puzzling: A clean ferromagnetic system cannot show a second order transition according to a no-go theorem within the Hertz-Millis-Moriya theory. A resoution to this puzzle, is that the transition here is not a ferromagnetic spin-density instability of heavy-electrons. Rather, this is a "local quantum critical point" in which the heavy-electrons disintegrate at the QCP, similar to the deconfined criticality in spin-systems.
- However, there is another puzzle: A ferromagnetic transition has a continuous evolution of the entanglement entropy and a continuous transition of the Fermi surface. Therefore, all the action should happen in spin-sector and anomalous charge behavior seen here, linear-in-T resistivity, would be absent in FM systems and would only show up in AFM systems.
- We found that the solution to this puzzle lies in another seemingly unrelated property of this material: The magnetic easy-plane anisotropy seen in magnetic susceptibility. Therefore, the magnetization is no longer a conserved quantity and develops marked zero-point fluctuations. In other words, magnetic anisotropy in ferromagnetic systems plays the same role as frustruation in anti-ferromagnetic systems.
- Indeed, we included magnetic anisotropy and found that a jump in the Fermi surface (appeared in the phase shift) can accompany a ferromagnetic transition.
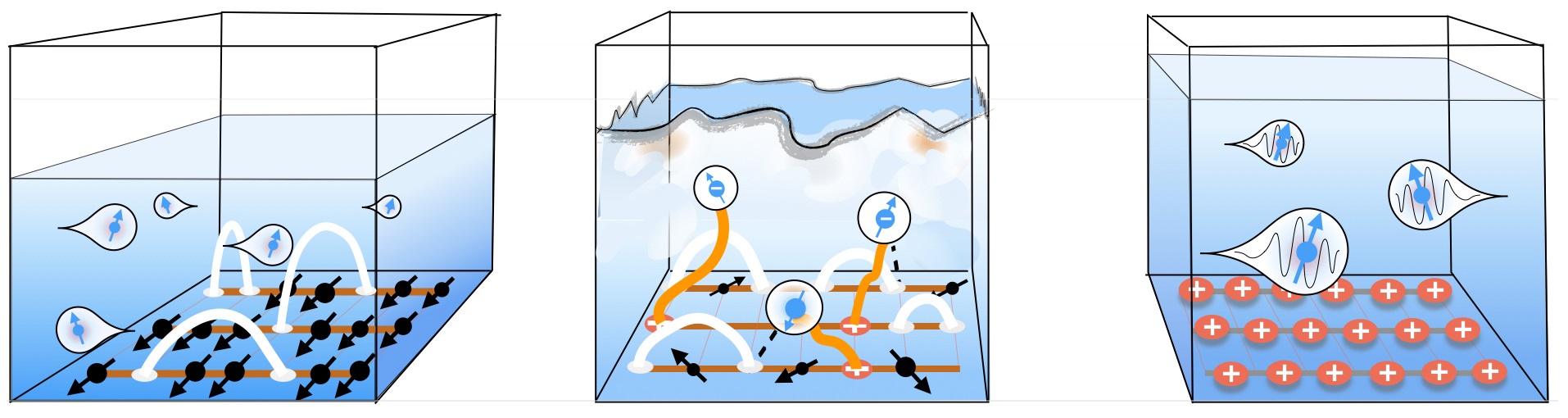
- This is the picture that emerged. On the left, the ferromagnetic ordred phase is not a product state. Rather, it contains triplet resonating valence bonds that entangle different spins. At the transition, the snapping of these tRVB states to form entanglement between the spins and the conduciton electrons leads to a jump in the Fermi surface. On the right, we have a larger Fermi surface produced by the spins.