Topological excitations and Small to Large Fermi Surface Transition
A. Wuglater, Y. Komijani, P. Coleman, , Large-N Approach to the Two-channel Kondo Lattice, ArXiv:1911.13129.
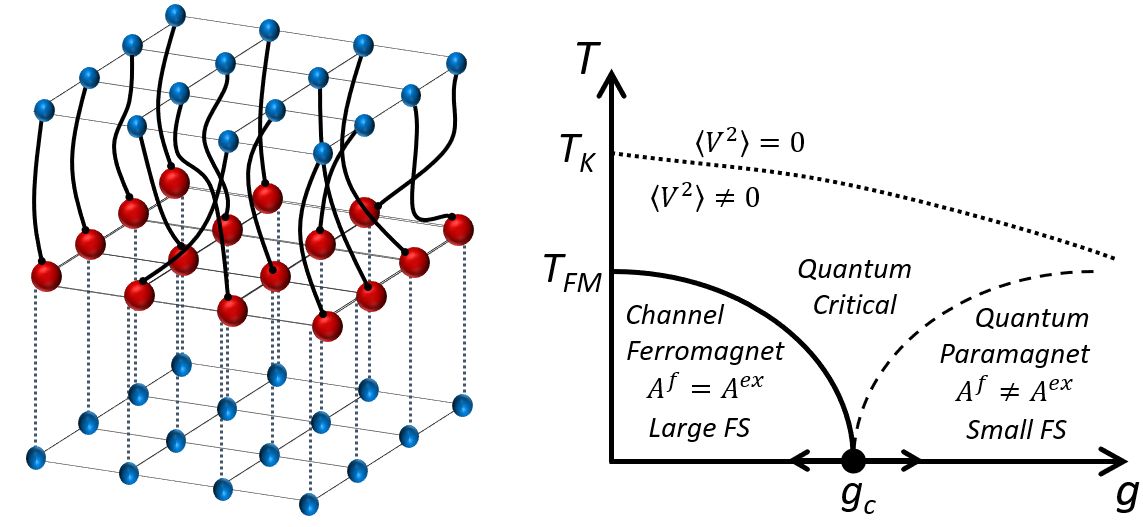
- We study the two-channel Kondo lattice in the large-N limit at half-filling using Abrikosov fermion representation of the spins. In this model, the continuous channel-symmetry is spontaneously broken, forming a channel ferromagnet in which one conduction channel forms a Kondo insulator, while the other remains conducting. (left figure).
- We discuss the relation between this solution and the Oshikawa's theorem, arguing that this ground-state can be understood using the concept of "order fractionalization", in which the channel magnetization breaks up into an emergent spinor order parameter.
- By integrating out the fermions we derive an effective action that describes this symmetry breaking and its emergent collective modes. A remarkable observation is that topological defects in the order parameter carry a U(1) flux, manifested in the Aharonov-Bohm phase picked by electrons that orbit the defect.
- By studying the effective action, we argue that the phase diagram contains a non-magnetic transition between a large and a small Fermi surface (where the topological defects proliferate) as shown in the right figure.
Fractionalized Order parameters
Y. Komijani, A. Toth, P. Chandra, P. Coleman, , Order Fractionalization, ArXiv:1811.11115.
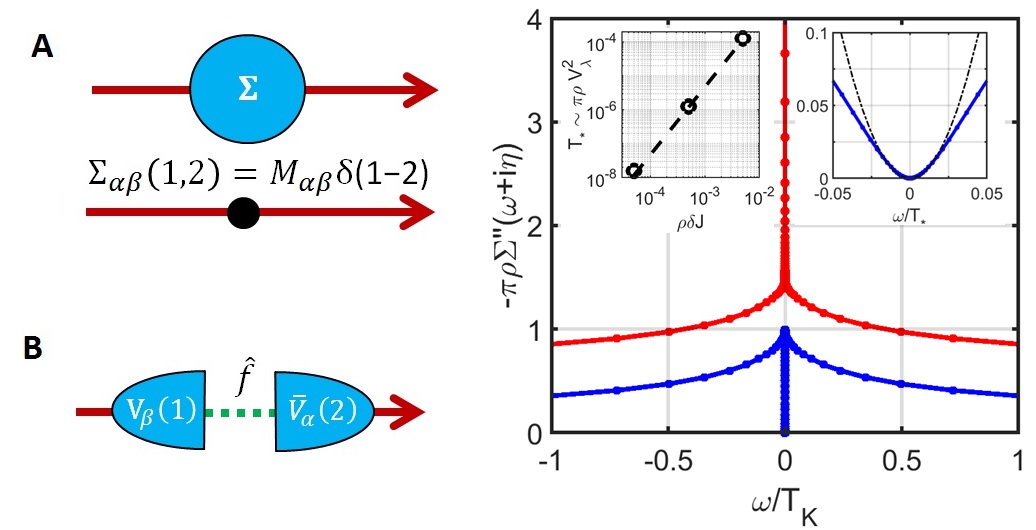
- Usual order parameters are characterized by off-diagonal long range order (ODLRO) and they can be characterized by the electronic self-energy which is local and instantaneous (left figure, top).
- Here, we extend the concept of ODLRO into the time domain, proposing that in a broken symmetry state, quantum operators can fractionalize into half-integer order parameters.
- This means that the electronic self-energy becomes a product of two spinorial order parameters and an intermediate fermionic resonance (figure left bottom).
- Using numerical renormalization group (NRG) studies we show how such fractionalized order can be induced in quantum impurity models. This is shown in the right figure, where a small channel aysmmetry leads to appearance of the fermionic resonance in one channel but not the other.
- We then conjecture that such order develops spontaneously in lattice quantum systems, due to positive feedback, leading to a new family of phases, manifested by a coincidence of broken symmetry and fractionalized excitations that can be detected by experiment.