Numerical inverse scattering for the Toda lattice

Jan 16, 2017·

Deniz Bilman

Thomas Trogdon

· 1 min read

Cite Code DOI ArXiv

Abstract

We present a method to compute the inverse scattering transform (IST) for the famed Toda lattice by solving the associated Riemann-Hilbert (RH) problem numerically. Deformations for the RH problem are incorporated so that the IST can be evaluated in $\mathcal{O}(1)$ operations for arbitrary points in the $(n, t)$-domain, including short- and long-time regimes. No time-stepping is required to compute the solution because $(n, t)$ appear as parameters in the associated RH problem. The solution of the Toda lattice is computed in long-time asymptotic regions where the asymptotics are not known rigorously.

Type

Journal article

Publication

Communications in Mathematical Physics 352, 2805–879, 2017

Time evolution of purely dispersive initial data is computed at $t=10000$ without time-stepping, at least by setting $t=10000$ in the Riemann-Hilbert problem and solving different Riemann-Hilbert problems as $n$ varies. Below are plots of $a_n$ (the off-diagonal of the bi-infinite Jacobi matrix) and $b_n$ (the diagonal of the bi-infinite Jacobi matrix).

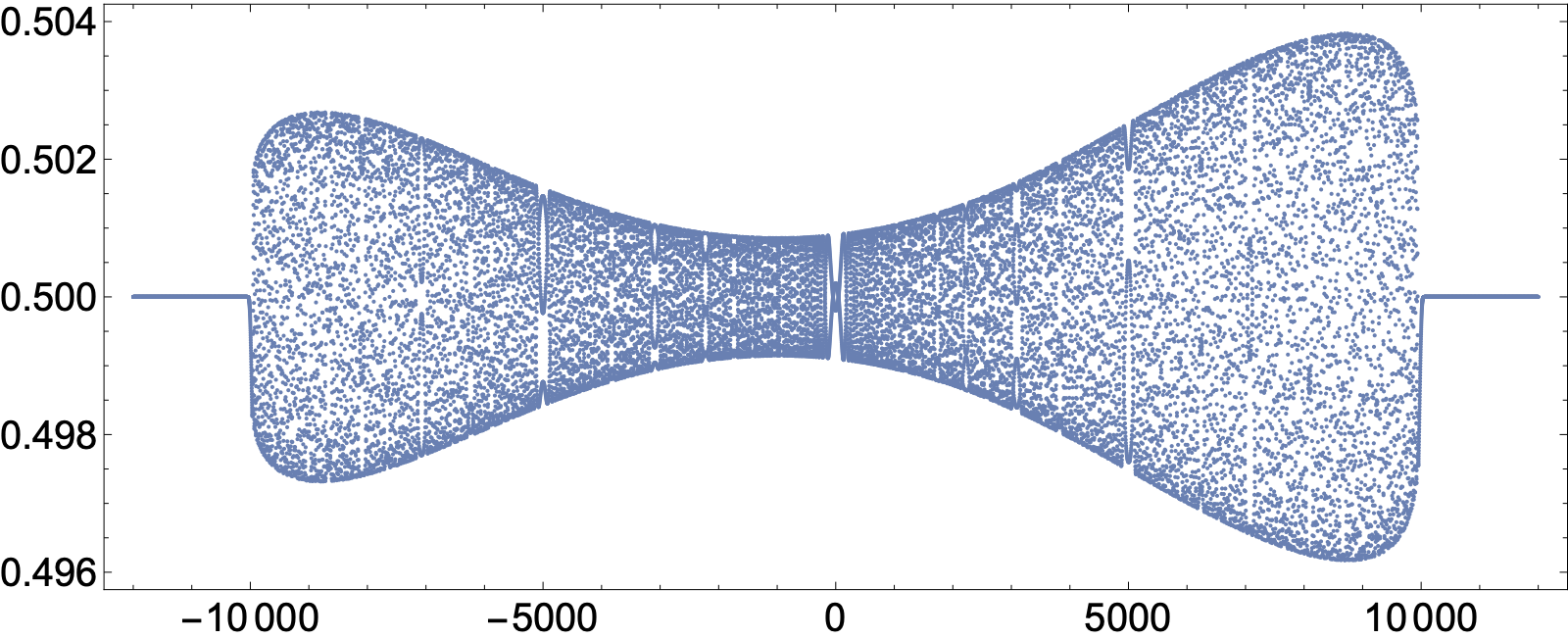
$a_n(t=10000)$, $-7500\leq n\leq 7500$. There are no solitons.

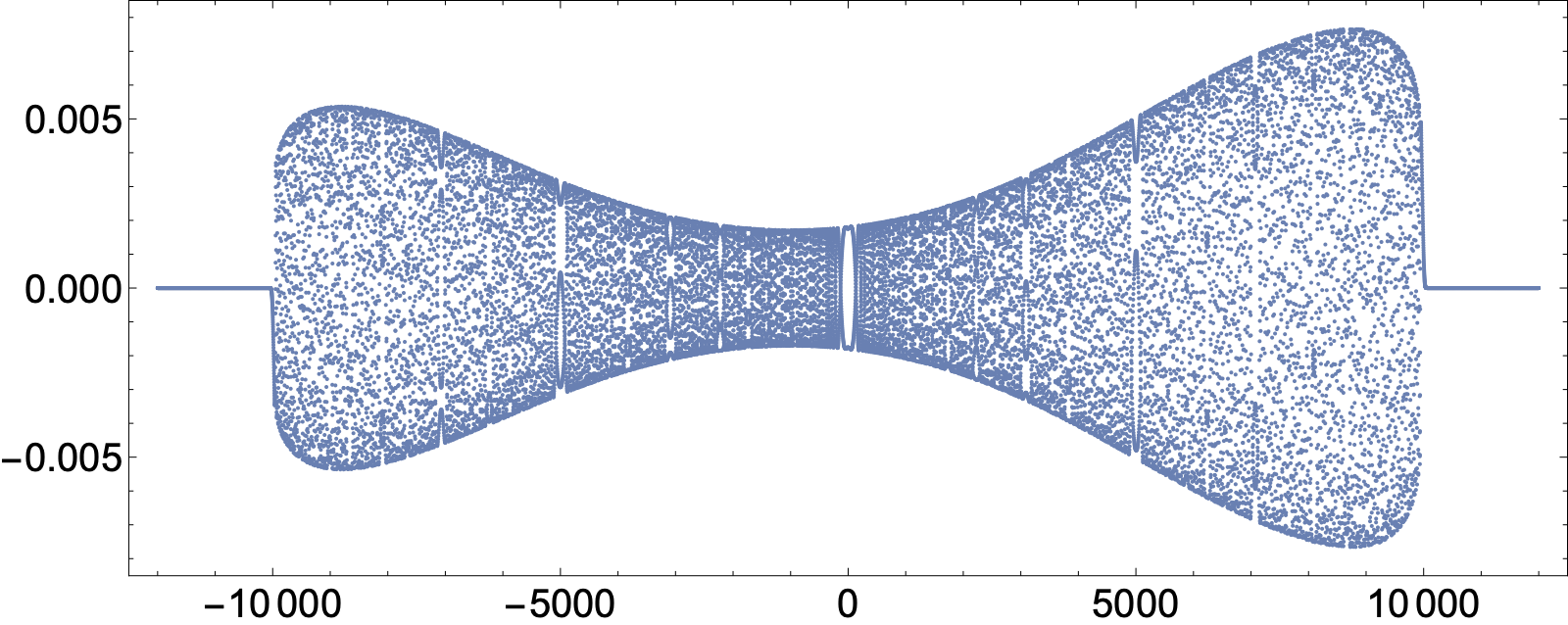
$b_n(t=10000)$, $-7500\leq n\leq 7500$. There are no solitons.

Below is the space-evolution of (truncated) contour for the Riemann-Hilbert problem that’s solved to compute the time evolution of initial data that generates a soliton to $t=1000$. Here $n$ varies from $n=-1250$ to $n=0$.

Time evolution of pure step (discontinuous) initial data

Last updated on Jan 16, 2017