Abstract
We present a method to compute the inverse scattering transform (IST) for the famed Toda lattice by solving the associated Riemann-Hilbert (RH) problem numerically. Deformations for the RH problem are incorporated so that the IST can be evaluated in $\mathcal{O}(1)$ operations for arbitrary points in the $(n, t)$-domain, including short- and long-time regimes. No time-stepping is required to compute the solution because $(n, t)$ appear as parameters in the associated RH problem. The solution of the Toda lattice is computed in long-time asymptotic regions where the asymptotics are not known rigorously.
Time evolution of purely dispersive initial data is computed at $t=10000$ without time-stepping, at least by setting $t=10000$ in the Riemann-Hilbert problem and solving different Riemann-Hilbert problems as $n$ varies. Below are plots of $a_n$ (the off-diagonal of the bi-infinite Jacobi matrix) and $b_n$ (the diagonal of the bi-infinite Jacobi matrix).
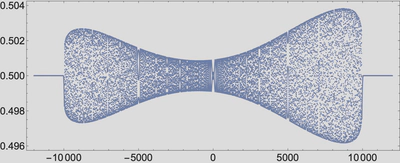

Below is the space-evolution of (truncated) contour for the Riemann-Hilbert problem that’s solved to compute the time evolution of initial data that generates a soliton to $t=1000$. Here $n$ varies from $n=-1250$ to $n=0$.