On numerical inverse scattering for the Korteweg-de Vries equation with discontinuous step-like data
Abstract
We present a method to compute dispersive shock wave solutions of the Korteweg–de Vries equation that emerge from initial data with step-like boundary conditions at infinity. We derive two different Riemann–Hilbert problems associated with the inverse scattering transform for the classical Schrödinger operator with possibly discontinuous, step-like potentials and develop relevant theory to ensure unique solvability of these problems. We then numerically implement the Deift–Zhou method of nonlinear steepest descent to compute the solution of the Cauchy problem for small times and in two asymptotic regions. Our method applies to continuous and discontinuous initial data.
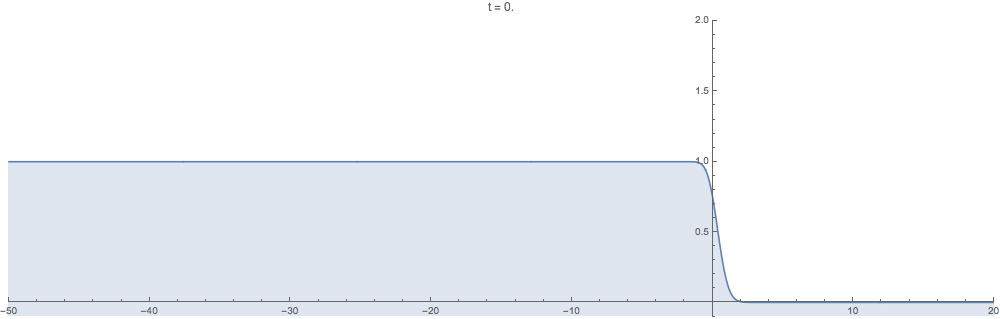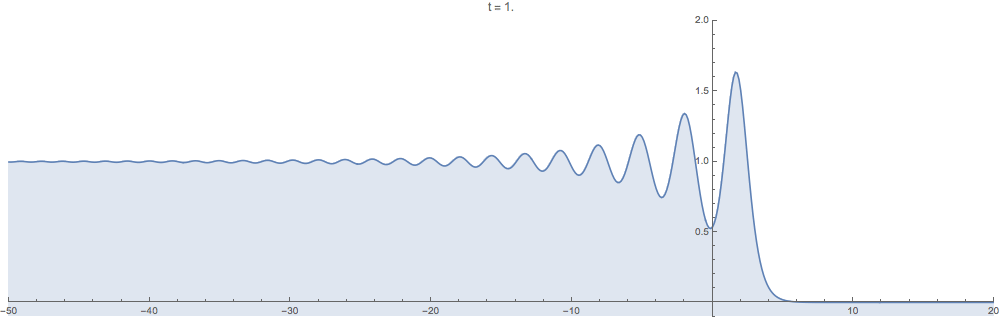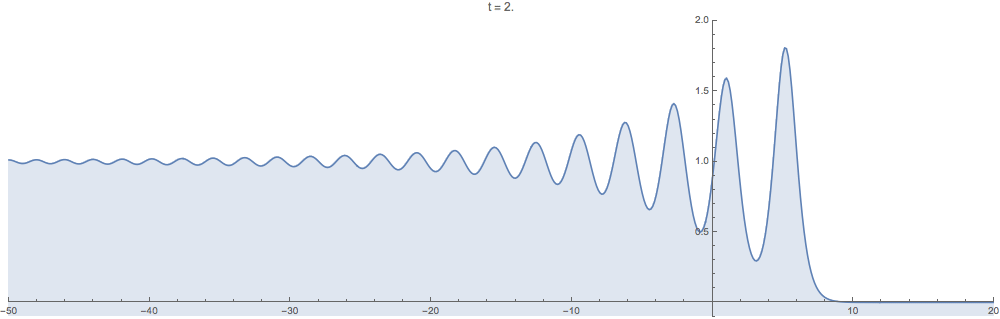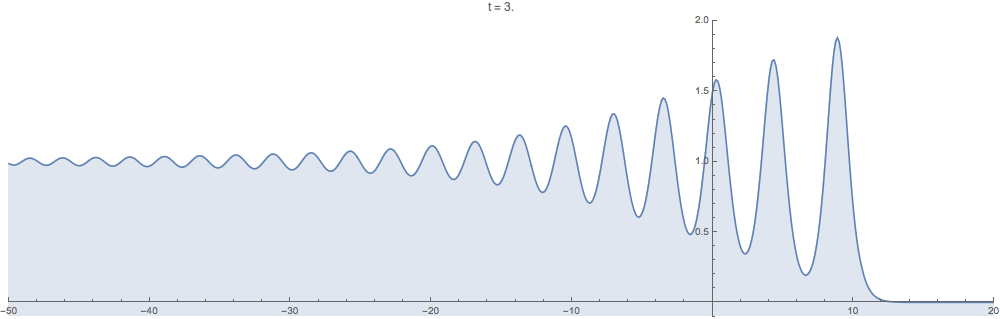
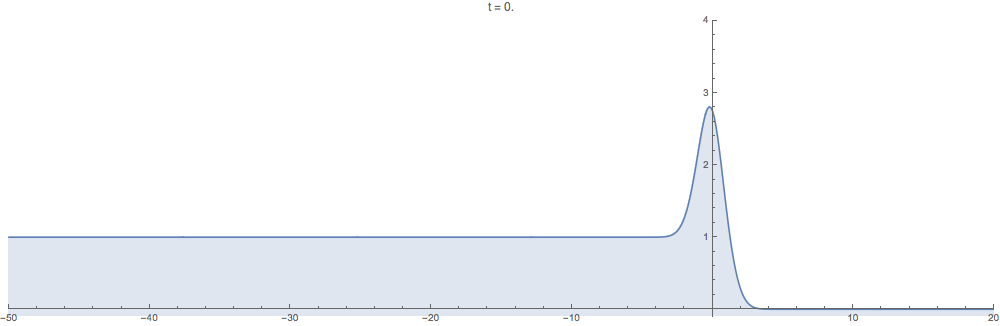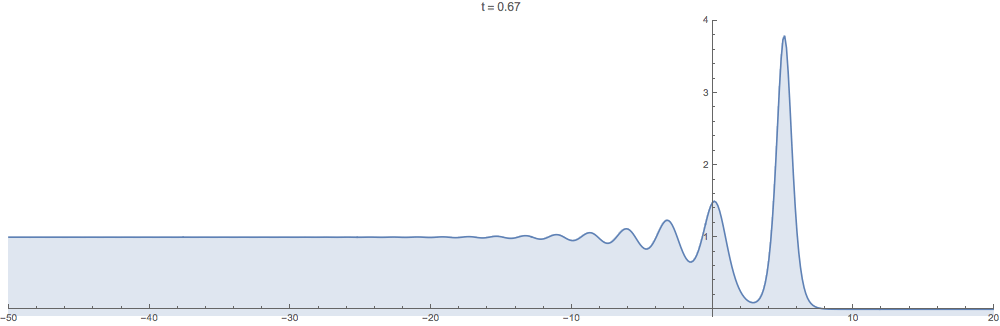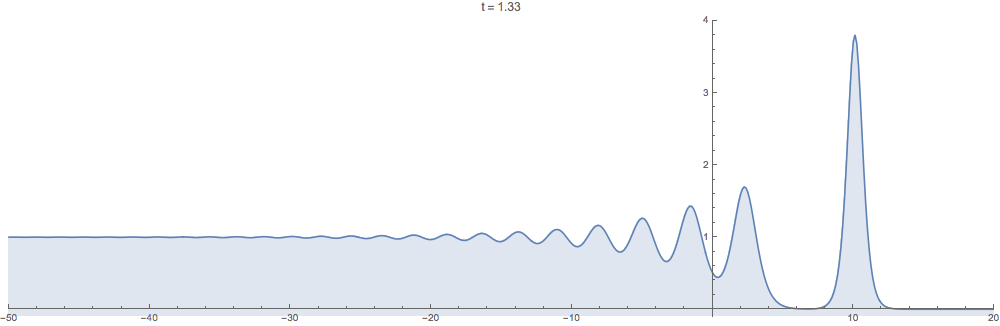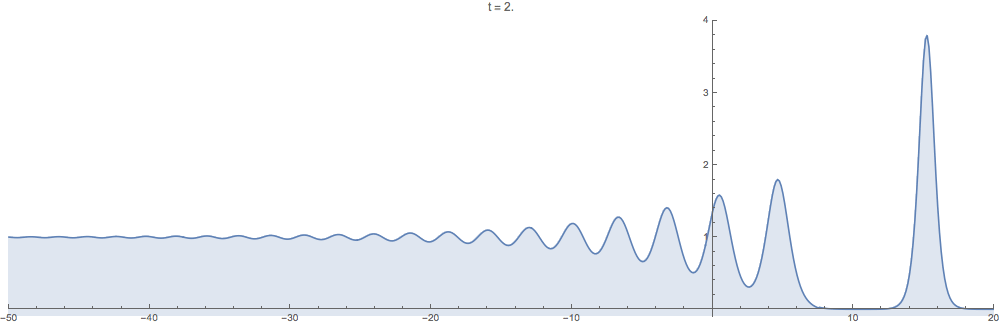
Supplementary animations generated with the computational method developed in this work are below. In all examples the initial data $u_0$ is step-like in the sense that $u_0(x)\to 0$ as $x\to +\infty$ but $u_0(x)\to c$ as $x\to -\infty$ for a positive constant $c>0$.