Extreme superposition: High-order fundamental rogue waves in the far-field regime

Abstract

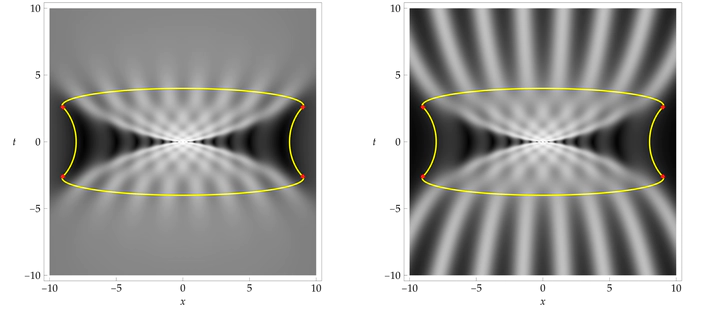
We study fundamental rogue-wave solutions of the focusing nonlinear Schrödinger equation in the limit that the order of the rogue wave is large and the independent variables $(x,t)$ are proportional to the order (the far-field limit). We first formulate a Riemann-Hilbert representation of these solutions that allows the order to vary continuously rather than by integer increments. The intermediate solutions in this continuous family include also soliton solutions for zero boundary conditions spectrally encoded by a single complex-conjugate pair of poles of arbitrary order, as well as other solutions having nonzero boundary conditions matching those of the rogue waves albeit with far slower decay as $x\rightarrow\pm\infty$. The large-order far-field asymptotic behavior of the solution depends on which of three disjoint regions $\mathcal{C}$, $\mathcal{S}$, and $\mathcal{E}$ contains the rescaled variables. On the regions $\mathcal{C}$ and $\mathcal{S}$ we show that the asymptotic behavior is the same for all continuous orders, while in the region $\mathcal{E}$ the discrete sequence of rogue-wave orders produces distinctive asymptotic behavior that is different from other cases.