Far-field asymptotics for multiple-pole solitons in the large-order limit
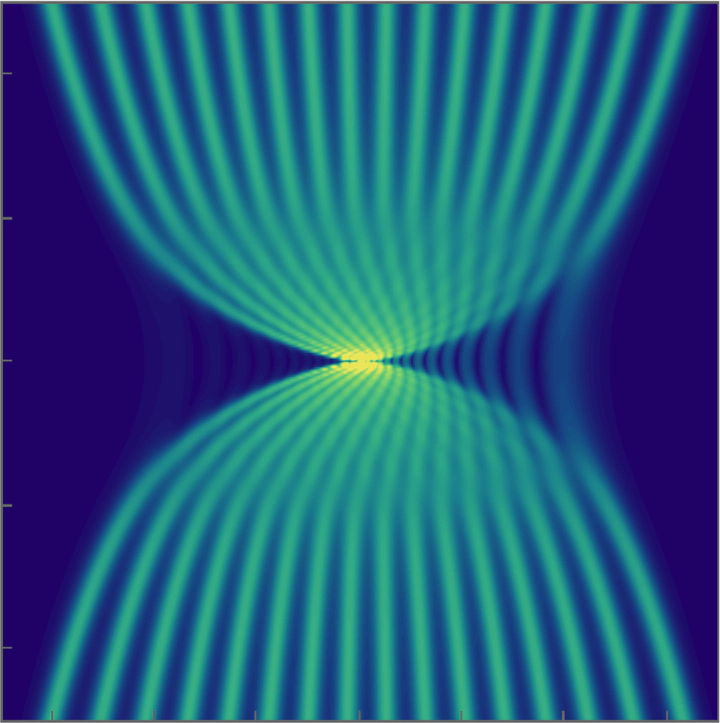 A multi-pole soliton of orde 16.
A multi-pole soliton of orde 16.
Abstract
The integrable focusing nonlinear Schrodinger equation admits soliton solutions whose associated spectral data consist of a single pair of conjugate poles of arbitrary order. We study families of such multiple-pole solitons generated by Darboux transformations as the pole order tends to infinity. We show that in an appropriate scaling, there are four regions in the space-time plane where solutions display qualitatively distinct behaviors; an exponential-decay region, an algebraic-decay region, a non-oscillatory region, and an oscillatory region. Using the nonlinear steepest-descent method for analyzing Riemann-Hilbert problems, we compute the leading-order asymptotic behavior in the algebraic-decay, non-oscillatory, and oscillatory regions.
Type
Publication
Journal of Differential Equations 297, 320–269, 2021