Computation of large-genus solutions of the Korteweg-de Vries equation
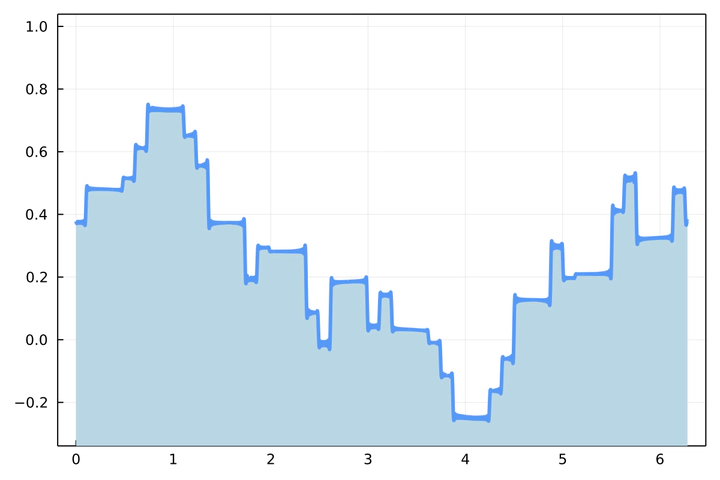 A manifestation of dispersive quantization in the nonlinear setting.
A manifestation of dispersive quantization in the nonlinear setting.
Abstract
We consider the numerical computation of finite-genus solutions of the Korteweg–de Vries equation when the genus is large. Our method applies both to the initial-value problem when spectral data can be computed and to dressing scenarios when spectral data is specified arbitrarily. In order to compute large genus solutions, we employ a weighted Chebyshev basis to solve an associated singular integral equation. We also extend previous work to compute period matrices and the Abel map when the genus is large, maintaining numerical stability. We demonstrate our method on four different classes of solutions. Specifically, we demonstrate dispersive quantization for “box” initial data and demonstrate how a large genus limit can be taken to produce a new class of potentials.
Type
Publication
Physica D 449 133715, 2022
As part of this work, we have constructed a solution of the Korteweg-de Vries equation by densely packing spectral bands inside a fixed interval. An animation of the resulting solution is given below. It seems to exhibit rogue-wave-type behavior on a periodic background.
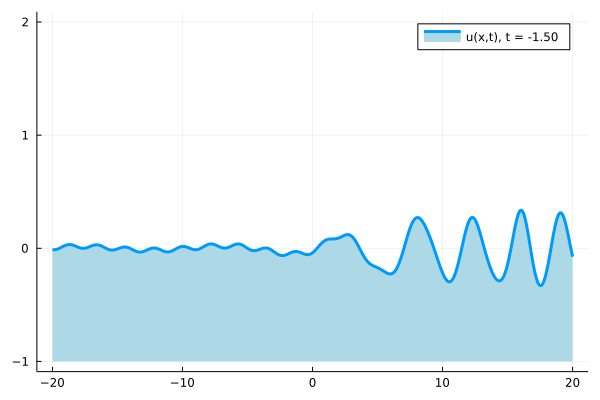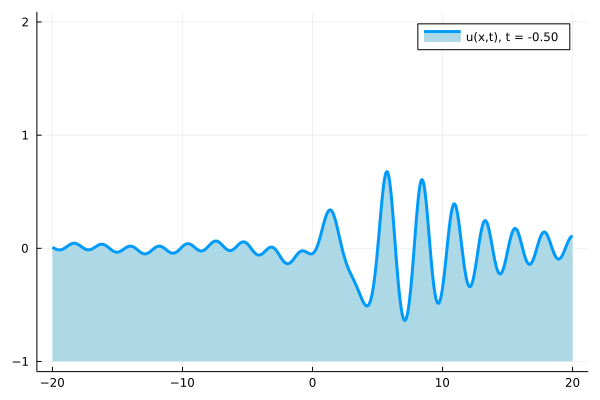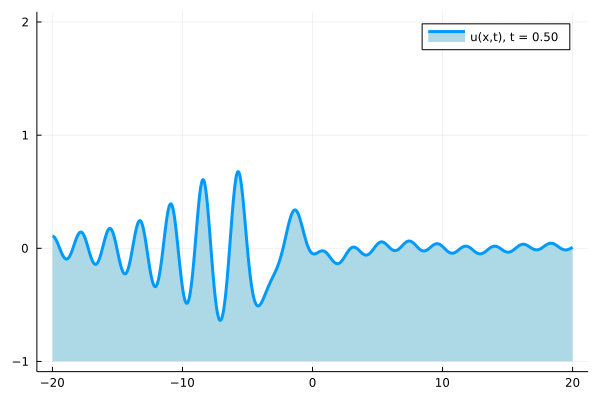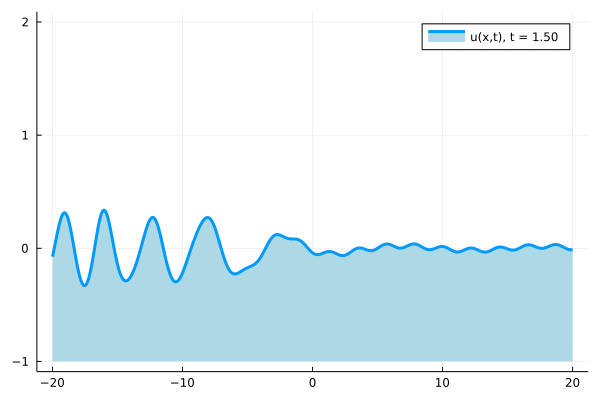
Time evolution of the solution constructed via accumulation of bands.
The contour plot of the same solution approximated by using $g=30$ gaps is given below.
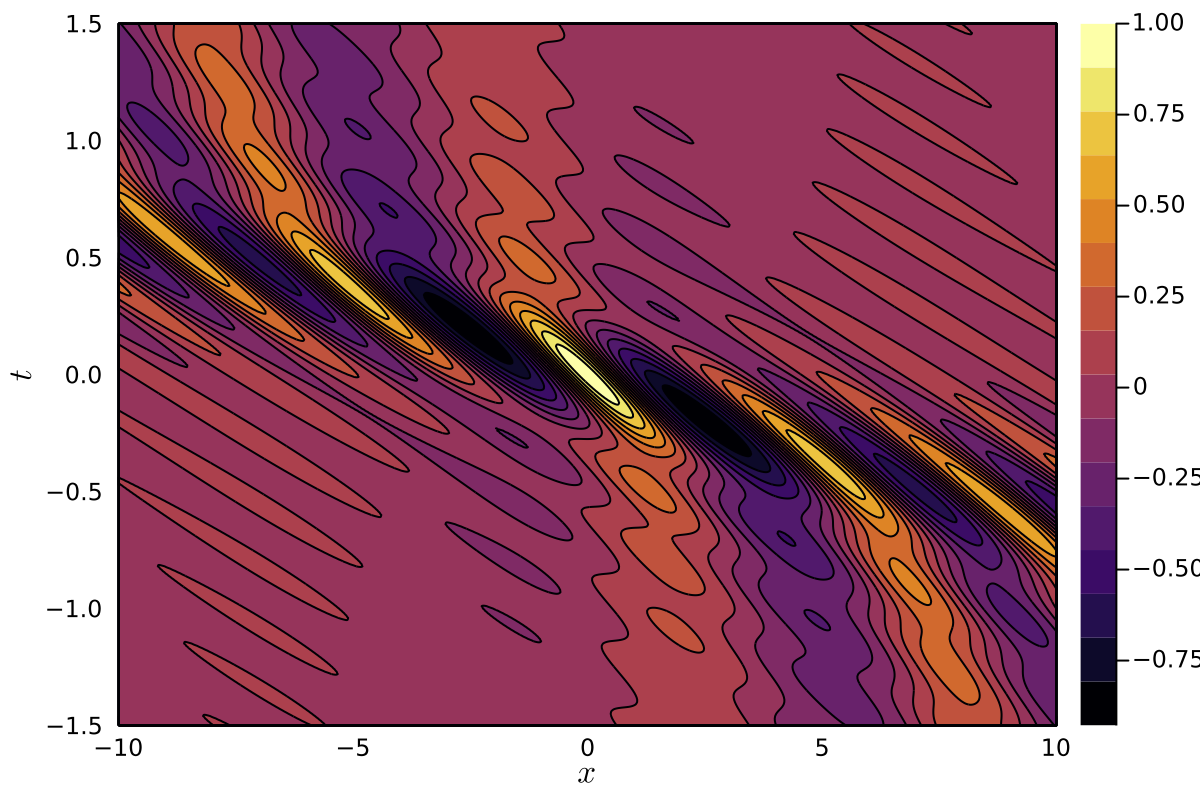
Time evolution of the solution constructed via accumulation of bands.
This work has also resulted in the software package PeriodicKdV.jl for Julia.