 Frank J. Pinski,
Department of
Physics, University of Cincinnati
Frank J. Pinski,
Department of
Physics, University of Cincinnati
Research Interests
The goal of my research is to develop a computational tool that can uncover
the pathway and the transition states that exist when a molecule changes
conformation or when it chemically changes. In many such circumstances, a
process must overcome an energy barrier before proceeding to completion. If the
size of the barrier is large compared to the available thermal energy, a
process must rely on the occurrence of one or more rare events. For such
circumstances, one would like to understand the reaction pathways so as to
improve yields, or as in the case of protein folding, to understand the
intermediate states. Many simple processes have been explored using theoretical
tools such as molecular dynamics, where the movements of individual atoms are
calculated. However, when the barrier is large, crossing the relevant barrier
is indeed a very rare event. Although computer speeds have been doubling every
18 months (a consequence of Moore's law), the exponentially long waiting times necessary for
barrier hopping pushes the required computational effort out of the feasibility
range for all but the simplest models. To explore these barrier-limited
processes, I am working with students and collaborators to develop a novel
computational technique to sample the paths themselves in a thermodynamically
significant manner.
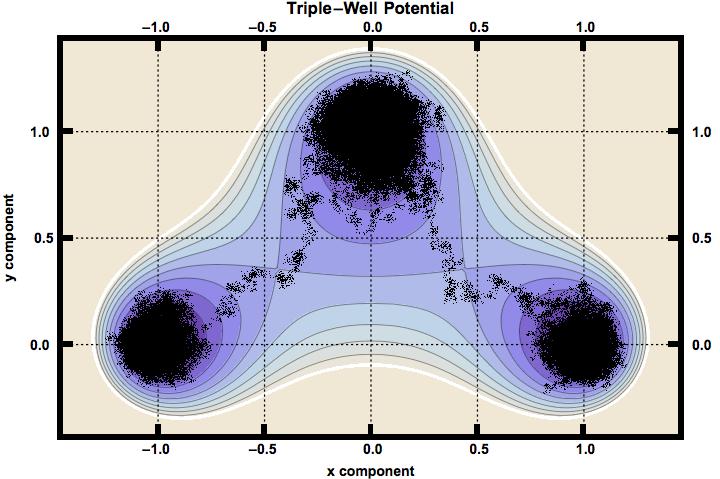
Above is an example of a transition path for a Brownian
particle moving in a potential consisting of three wells.
The bottom of the wells on the x axis
are at the potential zero, while the bottom of the well on the y-axis is
at a value of 0.25. The potential at the saddles is one.
The temperature is 0.20 in energy units.
The time length of the path is 62.5 units. The number of divisions along the path is 2^18.
The path starts in the well on the left and ends in the
well on the right but not before it stalls in the third well.
Note that the length of the path is short in that it
does not allow for multiple transitions.
Education
University of Minnesota, Physics, Ph.D., 1977
Advisor: Charles Campbell
Thesis:
Pair-pair correlations in simple fluids
Past Graduate Students
*
Duane Johnson, Ph.D., 1985.
Thesis:
The Electronic and Energetic Study of Magnetic, Random Substitutionally
Disordered Iron-Nickel Alloys
*
William A. Shelton, Jr., Ph.D., 1989.
Thesis:
The N-Atom Per Unit Cell Kkr-Cpa Applied to the Electronic Structure of
BARIUM(1-X) POTASSIUM(X) BISMUTH OXYGEN(3)
* John F. Clark, Ph.D., 1993.
Thesis:
A Study of Short-Range Order in Disordered Alloys
* Dereje Seifu
, Ph.D., 1994.
Thesis:
Energy of Ordered and Disordered Copper-Gold Alloys
* Mahdi Sanati,
Ph.D., 1999.
Thesis:
A theoretical study of the omega-phase transformation in metals
*
Manuel Valera, Ph.D., 2002.
Thesis:
Density functional study of classical liquids
* Thomas Maloney, M.S., 2010.
Thesis:
Adaptive Array-Gain Spatial Filtering in Magnetoencephalography
*
Patrick J. Malsom, Ph.D., 2015.
Thesis:
Rare Events and the Thermodynamic Action
Academic Lineage
N. Bowditch, Harvard University, 1802
B. Peirce, Harvard University, 1829
J. Lovering, Harvard University, 1833
J. Trowbridge, Harvard University, 1873
W. C. Sabine, Harvard University, 1890
P. W. Bridgman, Harvard University, 1908
E. C. Kemble, Harvard University, 1917
E. Feenberg, Harvard University, 1933
C. E. Campbell, Washington University (St. Louis), 1969
F. J. Pinski, University of Minnesota, 1977

Frank J. Pinski
EMAIL: frank dot pinski at uc dot edu
Contact Informaton
College Web Page
CV (two pages)
List of Publications
Google Scholar Profile
Recent publications
Role of Ito's lemma in sampling pinned diffusion paths in the continuous-time limit,
P.J. Malsom and F.J. Pinski,
Physical Reivew E 94 (4), 042131 (2016).
A function space HMC algorithm with second order Langevin diffusion limit,
Michela Ottobre, Natesh S. Pillai, Frank J. Pinski, and Andrew M. Stuart,
Bernoulli 22 (1), 60-106 (2016).
Algorithms for Kullback--Leibler Approximation of Probability Measures in Infinite Dimensions,
Frank Pinski, Gideon Simpson, Andrew Stuart, and Hendrik Weber
SIAM Journal on Scientific Computing 37 (6), A2733-A2757 (2015).
Kullback--Leibler approximation for probability measures on infinite dimensional spaces,
Frank Pinski, Gideon Simpson, Andrew Stuart, and Hendrik Weber,
SIAM Journal on Mathematical Analysis 47 (6), 4091-4122 (2015).
Gamma-Limit for Transition Paths of
Maximal Probability, F.J. Pinski, F. Theil and A.M. Stuart,
J. Stat. Phys. 146, 955–974 (2012);
doi:10.1007/s10955-012-0443-8
Hybrid Monte-Carlo on
Hilbert Spaces, A. Beskos, F.J. Pinski, J.-M. Sanz-Serna and
A.M.Stuart, Stoch. Proc. Applic.
121, 2201–2230 (2011); doi:10.1016/j.spa.2011.06.003
Transition paths in
molecules at finite temperature, F.J. Pinski and A.M. Stuart, J.
Chem. Phys. 132, 184104 (2010); doi:10.1063/1.3391160
Recent Talks and Posters
Poster:
Institute of Physics Condensed Matter Theory Group Meeting, 2011 (Coventry)
Poster:
IMA Workshop: Theory and Applications of Stochastic PDEs,2013 (Minneapolis)
Talk: ICIAM, 2011 (Vancouver)
Talk: AIMS, 2012 (Orlando)
Talk: Statistical Inference: Models in Physics and Learning, 2012 (Dresden)
Talk: Probability Seminar, UC Math Department, 2013 (Cincinnati)
Talk: MD Workshop, Warwick Mathematics Institute, 2013 (University of Warwick)
Talk: Seminar, The Institut de Physique Théorique, May 2014 (Saclay)
Talk:
Can we learn something important from wormy apples?
Talk:
Sampling Doubly Constrained Brownian Paths using HMC:
Exploring Entropic Barriers
Research Interests
The goal of my research is to develop a computational tool that can uncover
the pathway and the transition states that exist when a molecule changes
conformation or when it chemically changes. In many such circumstances, a
process must overcome an energy barrier before proceeding to completion. If the
size of the barrier is large compared to the available thermal energy, a
process must rely on the occurrence of one or more rare events. For such
circumstances, one would like to understand the reaction pathways so as to
improve yields, or as in the case of protein folding, to understand the
intermediate states. Many simple processes have been explored using theoretical
tools such as molecular dynamics, where the movements of individual atoms are
calculated. However, when the barrier is large, crossing the relevant barrier
is indeed a very rare event. Although computer speeds have been doubling every
18 months (a consequence of Moore's law), the exponentially long waiting times necessary for
barrier hopping pushes the required computational effort out of the feasibility
range for all but the simplest models. To explore these barrier-limited
processes, I am working with students and collaborators to develop a novel
computational technique to sample the paths themselves in a thermodynamically
significant manner.

Above is an example of a transition path for a Brownian particle moving in a potential consisting of three wells.
The bottom of the wells on the x axis are at the potential zero, while the bottom of the well on the y-axis is at a value of 0.25. The potential at the saddles is one.
The temperature is 0.20 in energy units. The time length of the path is 62.5 units. The number of divisions along the path is 2^18.
The path starts in the well on the left and ends in the well on the right but not before it stalls in the third well. Note that the length of the path is short in that it does not allow for multiple transitions.
Education
University of Minnesota, Physics, Ph.D., 1977
Advisor: Charles Campbell
Thesis:
Pair-pair correlations in simple fluids
Past Graduate Students
*
Duane Johnson, Ph.D., 1985.
Thesis:
The Electronic and Energetic Study of Magnetic, Random Substitutionally
Disordered Iron-Nickel Alloys
*
William A. Shelton, Jr., Ph.D., 1989.
Thesis:
The N-Atom Per Unit Cell Kkr-Cpa Applied to the Electronic Structure of
BARIUM(1-X) POTASSIUM(X) BISMUTH OXYGEN(3)
* John F. Clark, Ph.D., 1993.
Thesis:
A Study of Short-Range Order in Disordered Alloys
* Dereje Seifu
, Ph.D., 1994.
Thesis:
Energy of Ordered and Disordered Copper-Gold Alloys
* Mahdi Sanati,
Ph.D., 1999.
Thesis:
A theoretical study of the omega-phase transformation in metals
*
Manuel Valera, Ph.D., 2002.
Thesis:
Density functional study of classical liquids
* Thomas Maloney, M.S., 2010.
Thesis:
Adaptive Array-Gain Spatial Filtering in Magnetoencephalography
*
Patrick J. Malsom, Ph.D., 2015.
Thesis:
Rare Events and the Thermodynamic Action
Academic Lineage
N. Bowditch, Harvard University, 1802
B. Peirce, Harvard University, 1829
J. Lovering, Harvard University, 1833
J. Trowbridge, Harvard University, 1873
W. C. Sabine, Harvard University, 1890
P. W. Bridgman, Harvard University, 1908
E. C. Kemble, Harvard University, 1917
E. Feenberg, Harvard University, 1933
C. E. Campbell, Washington University (St. Louis), 1969
F. J. Pinski, University of Minnesota, 1977

Frank J. Pinski
EMAIL: frank dot pinski at uc dot eduContact Informaton
College Web Page
CV (two pages)
List of Publications
Google Scholar Profile
Recent publications
Role of Ito's lemma in sampling pinned diffusion paths in the continuous-time limit,
P.J. Malsom and F.J. Pinski,
Physical Reivew E 94 (4), 042131 (2016).
A function space HMC algorithm with second order Langevin diffusion limit,
Michela Ottobre, Natesh S. Pillai, Frank J. Pinski, and Andrew M. Stuart,
Bernoulli 22 (1), 60-106 (2016).
Algorithms for Kullback--Leibler Approximation of Probability Measures in Infinite Dimensions,
Frank Pinski, Gideon Simpson, Andrew Stuart, and Hendrik Weber
SIAM Journal on Scientific Computing 37 (6), A2733-A2757 (2015).
Kullback--Leibler approximation for probability measures on infinite dimensional spaces,
Frank Pinski, Gideon Simpson, Andrew Stuart, and Hendrik Weber,
SIAM Journal on Mathematical Analysis 47 (6), 4091-4122 (2015).
Gamma-Limit for Transition Paths of Maximal Probability, F.J. Pinski, F. Theil and A.M. Stuart, J. Stat. Phys. 146, 955–974 (2012); doi:10.1007/s10955-012-0443-8
Hybrid Monte-Carlo on Hilbert Spaces, A. Beskos, F.J. Pinski, J.-M. Sanz-Serna and A.M.Stuart, Stoch. Proc. Applic. 121, 2201–2230 (2011); doi:10.1016/j.spa.2011.06.003
Transition paths in molecules at finite temperature, F.J. Pinski and A.M. Stuart, J. Chem. Phys. 132, 184104 (2010); doi:10.1063/1.3391160
Recent Talks and Posters
Poster: Institute of Physics Condensed Matter Theory Group Meeting, 2011 (Coventry)
Poster: IMA Workshop: Theory and Applications of Stochastic PDEs,2013 (Minneapolis)
Talk: ICIAM, 2011 (Vancouver)
Talk: AIMS, 2012 (Orlando)
Talk: Statistical Inference: Models in Physics and Learning, 2012 (Dresden)
Talk: Probability Seminar, UC Math Department, 2013 (Cincinnati)
Talk: MD Workshop, Warwick Mathematics Institute, 2013 (University of Warwick)
Talk: Seminar, The Institut de Physique Théorique, May 2014 (Saclay)
Talk: Can we learn something important from wormy apples?
Talk: Sampling Doubly Constrained Brownian Paths using HMC: Exploring Entropic Barriers