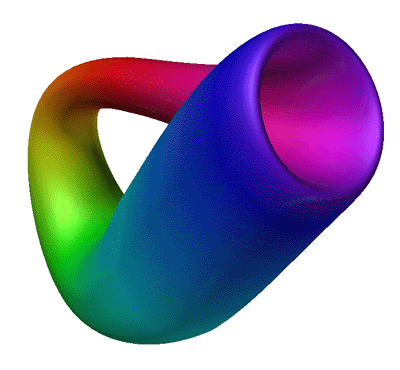|
Algebraic Topology
(15-Math-605) |
manifolds, topological groups, group actions, simplicial complexes, triangulations, polygon diagrams, polygonal presentations of surfaces, classification of compact surfaces, homotopy theory, homotopy equivalence, deformation retractions, fundamental group, mapping cylinders, covering spaces, unique lifting of homotopies, free products, amalgamation, Seifert-Van Kampen Theorem |
Department of
Mathematical
Sciences |
|
|
|
|
|
This page is a work in progress! (Last revised 3 January 2011)
Instructor Prof David A Herron
810D Old Chem Bldg, 556-4075 |
My Office Hours
Mon, Wed 12:30-1:45 and by appt |
E-mail me at David's e-address |
Link to a list of problems. |
Problem Session
TBA |
Below you can find information regarding: the current week's hot topics, some suggested problems, links to a number of interesting things, and the homework.
Textbooks
There are many topology texts available in the Geo-Math-Physics Library. I have placed some of these on open reserve---if you check one out at the end of the day, you can keep it over night.
Below I list the primary texts that I will use to generate my lectures; the order is somewhat indicative of how I will use these. It's a good idea to look at more than one book, because often some author will say things in just the 'right' way. Also, do not overlook the web as a resource; e.g., a google search on "identification spaces"---or just about any topic---will yield a number of interesting useful links.
For the most part, I will follow the text by Lee.
However, the book by Massey is the best place I know to learn about the fundamental group and related topics; if you can afford to, I recommend buying it. I personally really like Sieradski's book, and it covers point-set topology too. The book by Munkres is a great reference for point-set topology; you can prolly get it cheap on e-bay. Each of L, Ma, S, Mu, K, B covers the material that we will study Winter Quarter. The books by Hatcher and Bredon are somewhat more sophisticated than the rest, but are great references for Winter and Spring Quarters.
| L |
Lee |
Introduction to Topological Manifolds |
| Ma |
Massey |
Algebraic Topology: An Introduction |
| S |
Sieradski |
An Introduction to Topology and Homotopy |
| Mu |
Munkres |
Topology |
| K |
Kahn |
Topology, An Introduction to Point Set and Algebraic Areas |
| H |
Hatcher |
Algebraic Topology |
| B |
Bredon |
Topology and Geometry |
General Syllabus Chapters: 6-12 in L; 1-5 in Ma; 9-14 in S; 9, 11, 12 in Mu; 7-10 in K; 1,3 in B; 0,1 in H.
Course Goals
First and foremost, this course is an excursion into the realm of algebraic topology. Please take a few hours to review point-set topology; for the most part, chapters 1-5 of Lee (or 4-7 of Sieradski or 2-3 of Munkres or 3-6 of Kahn), contain the prerequisite information. Be sure you understand quotient and adjunction spaces.
We will begin with a whirlwind tour of the classification theory for compact surfaces. Then we'll look at homotopy theory and deformation retractions. Next we study the fundamental group. This will involve a detour to learn the basic of covering spaces, so that we can determine the fundamental group of the circle. Then we take another side trip to learn about free groups and free products, which will set us up to study the Seifert-Van Kampen theorem. Finally, we will return to undertake an in-depth look at coverings spaces.
A key idea throughout will be the use of algebraic techniques to understand topology. However, we'll also be able to turn this around and use topological information to gain insight into some algebra problems!
Of course I'll continue teaching you to think, act, and problem solve like a mathematician. Of particular importance, to me, is your continued improvement at communicating mathematical ideas effectively. This means learning to read, and especially to write, mathematical proofs. In addition, you should come to understand that different environments lend to different communication requirements.
A subgoal, at least for some of you, is preparation for the preliminary PhD examination in Topology; I will have (much) more to say about this in spring quarter (at which time I will run a prelim practice problem session). Here is the prelim syllabus. You can find copies of past prelim exams here.
Grades
Your final course grade will be determined from your performance on one midterm exam, a comprehensive final exam, some take-home quizzes, your homework scores, other possible written assignments, and your classroom and problem session participation. Roughly speaking, an A means that your work is at the PhD level, a B indicates masters level work, and anything less describes work that is not at the graduate level. Here is a precise breakdown:
- 35% --- final exam
- 30% --- one in-class hour exam
- 30% --- homework and written assignments
- 05% --- quizzes and class/problem session participation
The Final Exam is scheduled for Monday 14 March at 1:30-3:30. The in-class hour exam is (tentatively) scheduled for Monday 7 February. At certain unannounced classes I will distribute take-home quizzes that will be due before the next class.
Throughout Lee's book there are plenty of exercises; you should be sure to work all of these as well as the problems in the text. I will use some of these on the exams and quizzes.
I plan a long list of suggested problems for your Homework & Problem Session; these will be in addition to the textbook problems. We will have a weekly hour long problem session. Here I will expect you, the students, to present solutions to certain of the homework problems. We can also talk about other problems and/or topics from the lectures. If we have not done so beforehand, on the first day of class we will decide when to hold the problem session. I will also ask you write up and hand in solutions to certain exercises; these will be graded and returned to you. See below for due dates. I'll say more about this in class.
During the problem session, I will draw names at random (continuing until everyone has been chosen). When your name is chosen, I will ask you to work one of the suggested problems (see the table below). If you have nothing to say, you will receive -1; if your solution is valid, with sufficiently many details correct, you'll get +2; a partial solution will get you +1.
Here are some links to some interesting *things* such as videos, power point files, etc. I will add to this list as the year progresses.
The Möbius Band and Klein Bottle
- All you want to know about the Möbius Band.
- Some info about the Klein bottle.
- A colorful mpg showing how to cut open the Klein bottle.
- A youtube video showing great detail about the Klein bottle.
- A 5 minute youtube video discussing both the Möbius Band and the Klein Bottle.
Compact Surfaces
- Some surface experiments you can try.
- A youtube video illustrating things about a torus.
- A youtube video showing how to flatten a two-holed torus;
but the next item is much more informative!
- MrSuperTorus---a powerpoint presentation by Chantel C. Blackburn, a graduate
student in Mathematics at the University of Arizona. She also has a "mac" version.
If you like what she has created, please send her comments!
- A youtube topological trick.
Turning a Sphere Inside Out
Writing Mathematics
Class Stuff
Topics to be Covered Winter Quarter (although not necessarily in this order!)
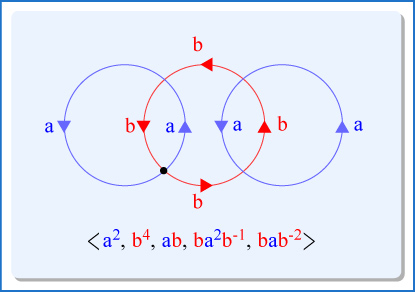
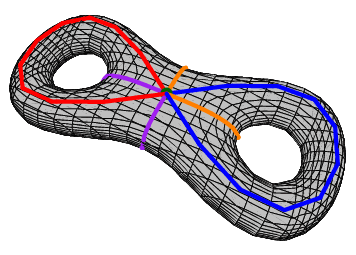
- Classification of Compact Surfaces
- basic examples: sphere, projective plane, torus, Klein bottle
- polygon diagrams and polygonal presentations
- handles, cross-handles, caps, cross-caps
- connected sums
- the catalog of all compact surfaces
- Homotopy Theory
- ideas and definition of homotopy, examples, essential maps versus null-homotopic ones
- equivalence relation and basic properties (e.g., naturality)
- relative homotopy
- contractible spaces
- deformation retractions and homotopy equivalence
- Fundamental Group
- homotopy of paths, concatenation, algebraic structure
- role of the basepoint
- simple connectivity
- fundamental group of circle
- fundamental group of sphere
- Seifert - Van Kampen Theorem
- fundamental groups of: wedges, compact surfaces
- Covering Spaces
- ideas and definitions, examples
- lifting problem: ULT, PLT, PHLT
- the FG of a CS, the conjugacy property
- lifting criterion
- equivalence of CS
- universal covering space
- group action property (monodromy)
- covering transformations
- normal covering spaces
- existence of covering spaces
- Applications
Some of the Topics Covered Autumn Quarter
- Topological Spaces
- topologies, bases, subbases
- open sets, closed set, limit points
- continuous maps, open maps, homeomorphisms
- Construction of Spaces
- product and quotient spaces
- identification spaces and group actions
- disjoint unions, wedge products, adjunction spaces
- simplicial complexes
- Manifolds
- basic definitions and examples
- Whitney's embedding theorem (baby version)
- connected sums, handles, cross handles, cross caps
- classifications of curves and closed surfaces
- Connected Spaces
- connected versus disconnected
- local connectivity
- path connected, locally path connected
- Compact Spaces
- compactness vs limit point compactness vs sequential compactness
- Weierstrass property
- local compactness
- compactifications
- Complete Metric Spaces
- completeness versus compactness
- total boundedness
- Heine-Borel property
- completions
- Baire category thoery
Some Topics NOT Covered but still Important
- Function Spaces
- pointwise convergence topology
- uniform convergence topology
- compact-open topology
- Arzela-Ascoli theorems
3-7 Jan We started by recalling the definition of a surface, and the quotient space constructions for the 2-sphere, the projective plane, the 2-torus, and the Klein bottle. Then we examined polygon diagrams and outlined a proof for the Pasting Theorem for Polygon Diagrams. We ended the week by listing all possible rectangle diagrams, and then defining the notion of a polygonal presentation.
10-14 Jan On Monday we saw several examples of polygonal presentations (some surface flattenings, some not), discussed the Pasting Theorem for Polygon Presentations, and defined the notion of a connected sum of two n-manifolds. On Wednesday we proved that the connected sum of two n-manifolds is another n-manifold. We discussed the notion of "attaching a handle" versus "attaching a cross-handle"; mostly this is in the HW. We also saw the statement of the Classification Theorem for Compact Surfaces. On Friday we looked at the connected sum of a torus with itself. Then saw how to present the connected sum of two polygon surface diagrams---that is, you just concatenate the boundary labels! We used this idea to see that attaching a handle to the projective plane is topologically equivalent to attaching a cross-handle; i.e. T^2 # P^2 is homeo to KB # P^2 which we already know is homeo to P^2 # P^2 # P^2. We completed Step I of the proof of the Classification Theorem for Compact Surfaces.
17-21 Jan Monday was MLK Day. On Wednesday we (mostly) finished the proof of the Classification Theorem for Compact Surfaces; I left Step VI for you to do, and just talked about Step VII. This provides a complete catalog of all compact surfaces. On Friday we started homotopy theory.
24-28 Jan On Monday we studied homotopy equivalence and deformation retractions, and then started relative homotopy. On Wednesday we should begin our investigation of the fundamental group.
31 Jan-4 Feb
7-11 Feb
14-18 Feb This week we learned a bunch of group theory: free products of groups, free groups, amalgamation, and presentations. All this group theory is just what we need in order to understand the content of the Seifert Van Kampen Theorem.
21-25 Feb We worked a few examples using the Seifert Van Kampen Theorem. Then we began our study of covering spaces. On Friday we proved the Unique Lifting Theorem, the Path Lifting Theorem, and saw the Path Homotopy Lifting Theorem.
28 Feb-4 Mar We outlined a proof of the Path Homotopy Lifting Theorem, and then saw some of its consequence including the Injectivity Property and the Action Property. We followed this by looking at the Conjugacy Property.
7-11 Mar Monday we saw the Lifting Criterion Theorem. During our last two lectures we
14-18 Mar This is Final Exams Week.
Below I list suggested problems for each indicated chapter in Lee. Don't forget to look at (i.e., work through) the many exercise placed throughout the book.
Here are suggested problems for each indicated section in Munkres.
- 51, Homotopy, p.330: 1-3
- 52, Fundamental Group, pp.354-355: 1,2,3,4,5,6
- 53, Intro to Covering Spaces, p.341: 1-6 all good
- 54, ULT, PLT, PHLT, pp.347-348: 1-3(do!),4,5,6-8 good too
- 55,56,57, Applications
- 58, Def Retracts and Homo Equiv, pp.366-367: 1&3(easy),2(fun!),4(do it!),5&6(easy),7,8
- 59, Fundamental Group of the Sphere, p.370: 1-2(good),3(easy),4good
- 60, Fundamental Groups of some Surfaces, p.375: 1-5 all good
- 67, Free Abelian Groups, p.412: 4
- 68, Free Products of Groups, p.412: 2,3
- 69, Free Groups, p.425: 1,3
- 70, Seifert-Van Kampen Theorem, p.433: 1,2,3
- 71, Wedge of Circles, p.438: 1,2,3,4,5
- 72,73,74, Compact Surfaces , p.445:1,2; pp.453-454:1-7
- 79, Equivalence of Covering Spaces, p.483:1-5
Unless I explicitly indicate otherwise, you should read everything in Lee's book and work all of the exercises that you find as you read. Any of these exercises, as well as all of the "fill in the details" that I mention during lectures, are fair game as "easy" exam questions.
Below is the assigned homework with due dates. (Here, again is a link to a pdf file for a list of these homework problems). The "Problems To Hand In" are to be written up and handed in before class on the indicated dates. The "For Session" problems will be discussed in that week's problem session. After the due date, you can find outlines for solutions (at least for some of the problems) by clicking the appropriate problem number.
Please be sure to check out my guidelines for writing up your HW solutions.
| Due Dates |
Problems To Hand In |
For Problem Session |
| 3,5,7 Jan |
First Day |
|
9(a,b,c) |
No Session |
| 10,12,14 Jan |
9(d,e),11,14,19 |
|
|
6,7,8,20,21,22 |
| 17,19,21 Jan |
MLK |
23,26 |
27 |
18,21,24,25,30(a),31(a) |
| 24,26,28 Jan |
24,25,29,30(b),31(b) |
|
|
19,32,34,36,38,39,40 |
| 31 Jan, 2,4 Feb |
19,33,35,41 |
|
37,44,47 |
34,42,43,45,46,48 |
| 7,9,11 Feb |
MidTerm |
|
49 |
48,50a,51,52,54,62 |
| 14,16,18 Feb |
50b,55,56,66 |
|
58 |
57,60,61,64,65,68 |
| 21,23,25 Feb |
59,69,72 |
|
|
Lee: p.191: 1,2,3,5,6; p.230: 1,4,7 |
| 28 Feb, 2,4 Mar |
82(a);Lee:8-6,10-7 |
|
77(S^2\cup I),80 |
53,74,77,81,82,83, Lee:10-1,2,3,4 |
| 7,9,11 Mar |
78,79,81 |
|
|
84,90,91,94,97(c),98,100,102,103 |
| 14 Mar |
Final Exam |
12:00-3:30 |
|
|