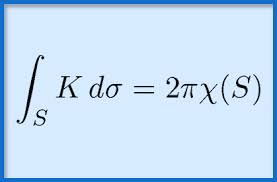Differential Geometry

(MATH 4012)

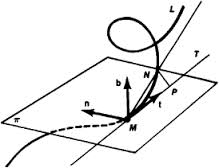
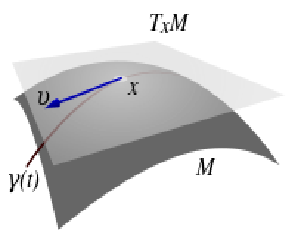
tangent vectors, tangent spaces, and the differential of a map; curves, surfaces, and hypersurfaces in Euclidean space; vector fields, differential forms, covariant derivatives, and connection forms; the Gauss map and shape operator; curvature; geodesics and the exponential map; Gauss, Bonnet, Hadamard

Department of

Mathematical

Sciences

This page is a work in progress! All information is subject to change (Last revised 23 January 2014)

Instructor Prof David A Herron
4514 French Hall, 556-4075 		My Office Hours
MWF 8:30-9:30 and by appt		 E-mail me at David's e-address
My web page is at David's w-address

Basic Course Information

Textbooks
I will follow the book Elementary Differential Geometry (revised 2nd edition) by Barret O'Neill; this is available from amazon (for about $57 new).

There are zillions of books about Differential Geometry available in the Geo-Math-Physics Library. Here are some "elementary" texts that I think are pretty good. See also the list of references an other notes that I provide below.
DC Manfredo DoCarmo Differential Geometry of Curves and Surfaces
S Michael Spivak A Comprehensive Introduction to Differential Geometry
T John Thorpe Elementary Topics in Differential Geometry
Here are some good books about differential topology, if you are interested.
L Lee Introduction to Smooth Manifolds
BJ Bröcker & Jänich Introduction to Differential Topology
GP Guillemin & Pollack Differential Topology
BT Barden & Thomas An Introduction to Differential Manifolds
C Conlen Differential Manifolds
K Kosinski Differential Manifolds
M Milnor Topology from the Differentiable Viewpoint
B Bredon Topology and Geometry

General Syllabus
I plan to cover the entire text, plus possibly some additional material.

Exams and Important Dates

Grades

Your final course grade will be determined from your performance on the in class exams, a comprehensive final exam, your homework scores on written assignments, and your classroom participation. Here is a precise breakdown:

The Final Exam is scheduled for Monday April 21 at 12:00-2:00pm. The in-class hour exams are (tentatively) scheduled the dates listed above.

Course Goals

The primary purpose of this course is to explore elementary differential geometry. Rather than a "theorem-proof" based course, we will strive to obtain a working knowledge of some of the basic concepts from differential geometry. The goal will be to foster the student's geometric intuition. Topics covered will include hypersurfaces in Euclidean space, tangent spaces and the differential of a map, differential forms, orientation, the Gauss map, curvature, vector fields, geodesics, the exponential map, the Gauss-Bonnet theorem, and other selected items.

Here are some links to some other references. I may add to this list as the year progresses.