Tides on Earth
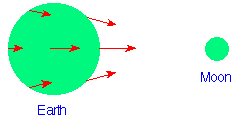 Moon exerts a gravitational
force on every object in/on the Earth. Tides occur because the
Earth is of a finite size (not infinitely small) and the forces
are not uniform, but depend on distance. Parts closer
to the Moon experience a larger gravitational tug than parts
further from the Moon.
These are called Differential Forces and they act on Earth
to distort it. The `solid' Earth is rather ridged, and distorts
only a bit (making the Earth somewhat `oblate').
The Oceans are more easily deformed, and this leads to the Ocean
tides seen.
Moon exerts a gravitational
force on every object in/on the Earth. Tides occur because the
Earth is of a finite size (not infinitely small) and the forces
are not uniform, but depend on distance. Parts closer
to the Moon experience a larger gravitational tug than parts
further from the Moon.
These are called Differential Forces and they act on Earth
to distort it. The `solid' Earth is rather ridged, and distorts
only a bit (making the Earth somewhat `oblate').
The Oceans are more easily deformed, and this leads to the Ocean
tides seen.
 A Simple Tidal Model
A Simple Tidal Model
Imagine a planet entirely covered with Ocean. Point A (on the left) is
closer to the Moon and experiences a larger gravitational force
than point B or point C. Point A is pulled away from the Earth,
toward the Moon, thus producing the bulge on the right side.
The left side bulge arises because the Earth is
pulled away because the moon's gravitational force
at point B is larger than at point C. As Earth
rotates, a given point on its surface
will experience two high and two low tides for each
rotation of the planet.
 Tides in Real Life.
Tides in Real Life.
The tides seen at a given location is a bit more complex.
Latitude, shape of shore, depth of ocean and inlets, winds, all
effect the tide amount. Typical tides are a meter or
two. The Bay of Fundy, in Nova Scotia Canada, experiences tides
40 feet! The Gulf of
California (Sea of Cortez) has 24-foot tides at the top of the
bay. The Gulf of Mexico experiences just one, 1-foot, tide per day!
The largest tides are experienced when the Sun and the Moon are lined up with the Earth (new and full phases of the Moon). These are called Spring Tides (the name is not associated with the season of Spring).
Orbital Effects
It takes energy to lift up all that water. This energy loss has
slowed down the rotation of the Moon AND moved the Moon
further away from the Earth (at a rate of 4cm a year right
now). 3 billion years ago, the Moon orbited the Earth in just 17 days!
The moon is now in synchronous rotation (same face always towards us).
Nearly all moons in the Solar System experience this.
As a consequence of tidal interactions with the Moon, the Earth's rotational period is also slowly decreasing. 109 yrs ago, a day was just 18 hours long! Eventually the Earth will slow to where it and the Moon will have the same rotational (and orbital) period and will always face each other.
If a moon gets close to a very massive planet, the difference between gravitational force on the near side of the moon compared to the far side can be great enough to pull it apart! Any object which gets too close to a massive object, within its Roche limit, will be torn apart.