The Fifth Ohio River Analysis Meeting

Roza Aceska (Ball State): Weight functions with directional sensitivity.

We study new properties of a recently introduced, directionally sensitive short-time Fourier transform. Its specific relationship to the classical short-time Fourier transform and its quasi shift-invariance property motivate us to introduce customized weight functions with directional sensitivity. (joint work with H.H. Giv)

Ryan Alvarado (Missouri): A sharp theory of Hardy spaces in spaces of homogeneous type.

One significant step in the development of the theory of Hardy spaces (H^p spaces) was the consideration of H^p defined on an environment which, structurally speaking, is much more general than the Euclidean ambient. In this talk I will present some recent progress with M. Mitrea detailing a sharp H^p-theory in the abstract setting of spaces of homogeneous type. More specifically, in the above context we will introduce Hardy spaces defined via a grand maximal function and prove that a satisfactory H^p-theory exists for an optimal range of p's, which depends on both the geometric and measure theoretic aspects of the ambient. Many facets of this theory will be discussed including sharp versions of several tools used in the area of analysis on spaces of homogeneous type such as a sharp Lebesgue differentiation theorem.

Thomas Bieske (South Florida): The p(x)-Laplacian on Carnot groups.

We discuss existence-uniqueness of viscosity solutions to the p(x)-Laplace equation in Carnot groups.

Miguel Caicedo (Cincinnati): Well-posedness of a nonlinear boundary value problem for the KdV equation on a finite domain.

In this talk we consider an initial boundary value problem for the Korteweg-de Vries equation posed on a finite interval, I=(0,L), with a non-linear boundary condition at the left end point of the interval. It will be shown that this initial boundary value problem is locally well-posed in the L²-based Sobolev space H^s(0,L) for any s≥0.

Dat Cao (Missouri): Finite energy and weak solutions of sublinear elliptic equations.

We study finite energy and weak solutions to the homogeneous quasilinear elliptic equations -Δ_p u = σ u^q   on Rⁿ in the case 0 < q < p-1, where Δ_p u = ∇ · (∇u |∇u|^p-2) is the p-Laplacian and σ is a nonnegative function (or measure) on Rⁿ. We will present the necessary and sufficient conditions for the existence of positive solutions, together with bilateral pointwise estimates. We also discuss the regularity and uniqueness questions. This is joint work with Igor E. Verbitsky.

Dewey Estep (Cincinnati): Geometry of the prime end boundary and the Dirichlet problem for bounded domains in metric measure spaces.

First introduced in the complex plane by Caratheodory, prime ends provide a way to define the boundary of a bounded domain such that its closure retains many properties intrinsic to the structure of the domain itself, rather than its ambient space. For example, the prime end closure of the slit disk in \(\mathbb{C}\) retains the structure imposed by the 'slit', while the normal metric closure ignores it. Using a slight modification of the definition given by Adamowicz, Björn, Björn, and Shanmugalingam, we may study prime ends in more general metric spaces. Here we define and study the dirichlet problem with prime end boundary data on bounded domains, showing that under certain assumptions we may construct solutions using the Perron method.

Lila Greco (Kenyon): Brownian motion in the complex plane.

This project explores Brownian motion, a model of random motion, in the plane. Given a domain in the complex plane and a basepoint in the domain, start a Brownian traveler at that basepoint. The h-function of the domain gives information about where the Brownian traveler is likely to first hit the boundary of the domain. I will give examples of h-functions I computed for several families of domains. Next I will describe a connection between the geometry of domains and their h-functions. I will present results about the convergence of a sequence h-functions. Finally, I will end with approximating h-functions using simulations of Brownian motion.

Piotr Hajłasz (Pittsburgh): Maximal functions, Littlewood-Paley theory and Sobolev spaces.

I will talk about new characterizations of the Sobolev spaces that involve the Littlewood-Paley theory. I will also advertise open problems about boundedness of the maximal functions in Sobolev spaces. The talk is based on my joint papers with Zhuomin Liu and Jan Maly.

John Helms (UC Santa Barbara): Global solutions to 2-D quasilinear wave equations.

This work is in joint collaboration with Professor Thomas Sideris (UCSB). We consider small-data solutions to equations of the form 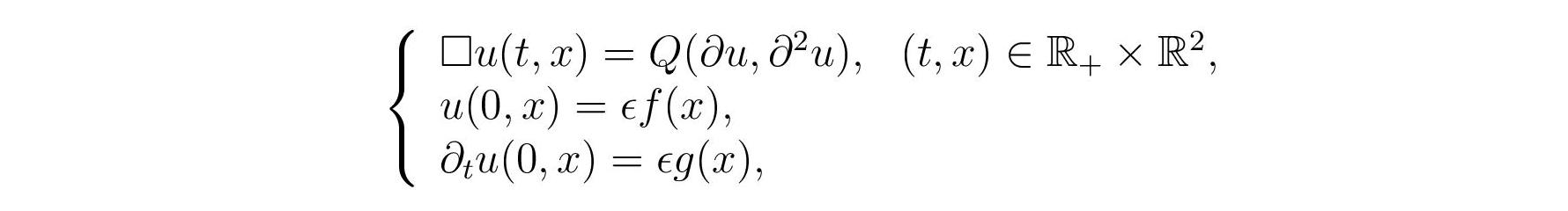where □ = ∂_t² - Δ and the nonlinearity Q is allowed to depend on ∂u and ∂²u at the quadratic level and higher. We also assume that Q is linear in ∂²u and that Q satisfies a null condition, which is due to Christodoulou and Klainerman. Alinhac proved global existence of small-data solutions with smooth, compactly supported data (f,g) by using a "Ghost weight" in his main energy estimate. Our proof extends Alinhac's result by allowing for a weaker hypothesis on the initial data: (f,g) are only required to have a certain amount of weighted Sobolev regularity with no restrictions on the support. Our proof also eliminates the use of the Lorentz boosts x_i∂_t + t∂_i (i = 1,2) from the existence argument.

Jay Hineman (Fordham): Very weak solutions for Poisson-Nernst-Planck system.

We formulate a notion of very weak solution for the Poisson–Nernst–Planck system. The Poisson–Nernst–Planck system describes the motion of ions due to diffusion and electromigration. The stationary system possesses a local monotonicity formula which reveals a local boundedness result for ion density and the gradient of electrical potential. These results are part of recent joint work with Rolf J. Ryham.

Joshua Isralowitz (Albany): Matrix weighted Poincare and Sobolev inequalities.

With an eye towards proving new regularity results for degenerate systems of elliptic PDEs, we prove natural matrix weighted Poincare and Sobolev inequalities that are closely related to the classical Fabes/Kenig/Serapioni scalar weighted Poincare and Sobolev inequalities. Furthermore, we prove natural matrix weighted norm inequalities for both the classical fractional integral operators and fractional maximal operators. This is joint work with Kabe Moen.

Paata Ivanishvili (Michigan State): Lerner's inequality in arbitrary dimension.

Svetlana Jitomirskaya (UC Irvine): Quasiperiodic operators with monotone potentials: sharp arithmetic spectral transitions and small coupling localization.

It is well known that spectral properties of quasiperiodic operators depend rather delicately on the arithmetics of the parameters involved. Consequently, obtaining results for all parameters often requires considerably more difficult arguments than for a.e. parameter, and does offer a deeper insight. In the first part of the talk we will report the first result of this kind in regard to the spectral decomposition: full description of spectral types of the Maryland model for all (in contrast with almost every, known for ~30 years) values of frequency, phase, and coupling (with nontrivial dependence on the arithmetics). In the second part of the talk we show that for (a large class of) bounded monotone potentials there is Anderson localization for all non-zero couplings.

Kay Kirkpatrick (Illinois): Bose-Einstein condensation: from many quantum particles to a quantum "superparticle."

Near absolute zero, a gas of quantum particles can condense into an unusual state of matter, called Bose-Einstein condensation (BEC), that behaves like a giant quantum particle. The rigorous connection has recently been made between the physics of the microscopic many-body dynamics and the mathematics of the macroscopic model, the cubic nonlinear Schrodinger equation (NLS). I'll discuss progress with Gerard Ben Arous and Benjamin Schlein on a central limit theorem for the quantum many-body dynamics, a step towards large deviations for Bose-Einstein condensation.

Nguyen Lam (Pittsburgh): Sharp Moser-Trudinger-Adams inequalities.

Moser-Trudinger and Adams inequalities have received important attention in recent years. In this talk, we present some recent development on sharp Moser-Trudinger type inequalities on first order Sobolev spaces and sharp Adams type inequalities on high order Sobolev spaces on both Euclidean spaces and Heisenberg groups. Since the symmetrization argument is not available on these settings, we propose a rearrangement-free method to study these sharp inequalities. This talk is based on joint works with Guozhen Lu and Hanli Tang.

Phi Le (Missouri): Carleson measure estimate and Dirichlet problems for degenerate elliptic equations.

In this project, we were interested in Carleson measure estimates and the solvability of Dirichlet problem for degenerate elliptic equations. More precisely, we proved that if u is a bounded solution of the elliptic equation Lu= - div A∇u = 0 in the domain \({\textbf R}^{n+1}_+\) where the elliptic matrix A is t-independent, not necessarily symmetric, and satisfies the weighted ellipticity condition

λ μ(x)|ξ|2 ≤ 〈A(x)ξ, ξ 〉 ≤ μ(x)Λ|ξ|2

where μ is in Muckenhoupt A₂ class. Then u satisfies the weighted Carleson measure estimate \[ \sup_Q \frac1{\mu(Q)} \int_Q \int_0^{\ell(Q)} |\nabla u(x,t)|^2\, t dt\, \mu(x) dx \leq C \|u\|^2_\infty\nonumber \] Once we have the weighted Carleson measure estimate, we deduce the corresponding square function is bounded by nontangential maximal function, the harmonic measure is in A_∞ class with respect to surface measure and also the solvability of the Dirichlet problem (D)_p for some p >1.

( joint work with Steve Hofmann and Andrew Morris).

Jungang Li (Wayne State): Best constants for Moser's inequality on noncompact Riemannian manifolds.

We will consider the sharp Moser-Trudinger inequality on complete noncompact Riemannian manifolds. Namely, \[ \sup_{u\in W^{1,n}(M), ||u||_{1,\tau}\leq 1}\int_M \phi(\alpha_n|u|^{\frac{n}{n-1}})dV_g\leq C(n,\tau) \] Where \( \phi(t)=\sum_{k=n-1}^{\infty}\frac{t^k}{k!}\), \(\alpha_n=n\omega_{n-1}^{\frac{1}{n-1}}\), where ω_n-1 is the area of the unit sphere in Rⁿ, \(||u||_{1,\tau}=(\int_M \tau|u|^n+|\nabla u|^n)^{\frac{1}{n}}\). The inequality is sharp in the sense that for α > α_n, the above inequality fails.

Xining Li (Cincinnati): Preservation of bounded geometry under sphericalization and flattening: quasiconvexity and ∞-Poincare inequality.

This is a joint work with Estibalitz Durand-Cartagena. In this work we explore the preservation of quasiconvexity and ∞-Poincare inequality under sphericalization and flattening in the metric setting. The results developed in our previous work show that the Ahlfors regularity, doubling property, and the p-Poincare inequality for p < ∞ are preserved under the sphericalization and flattening transformations if one assumes the underlying metric space has annular quasicovexity. In this work, we propose a weaker assumption to still preserve quasiconvexity and ∞-Poincare inequality, called radial starlike quasiconvexity and meridian starlike quasiconvexity, extending in particular a result by Buckley, Herron and Xie to a wider class of metric spaces and covering the case p = ∞ in our previous work.

Alex Misiats (Purdue): Invariant measures for stochastic reaction-diffusion equations.

We study the long-time behavior of systems governed by nonlinear reaction-diffusion type equations du = (Au + f(u))dt + σ(u) dW(t), where A is an elliptic operator, f and σ are nonlinear maps and W is an infinite dimensional nuclear Wiener process. This equation is known to have a uniformly bounded (in time) solution provided f(u) possesses certain dissipative properties. The existence of a bounded solution implies, in turn, the existence of an invariant measure for this equation, which is an important step in establishing the ergodic behavior of the underlying physical system.

In my presentation I will talk about expanding the existing class of nonlinearities f and σ, for which the invariant measure exists. We also show that the equation has a unique invariant measure if A is a Schrödinger-type operator A = 1/ρ (div ρ∇u) where ρ = e^-|x|2 is the Gaussian weight. In this case the source of dissipation comes from the operator A instead of the nonlinearity f. The main idea is to show that the reaction-diffusion equation has a unique bounded solution, defined for all t ∈ R, i.e. that can be extended backwards in time. This solution is an analog of the trivial solution for the linear heat equation.

Michael Music (Kentucky): Solutions to the Novikov-Veselov equation via the inverse scattering method.

Using the inverse scattering method, we construct global solutions to the Novikov-Veselov equation at zero energy for decaying initial data q₀ with the property that associated Schrödinger operator (-∂∂ + q)  is nonnegative. These results considerably extend previous results of Lassas-Mueller-Siltanen-Stahel and Perry. Our analysis draws on previous work of the first author and on ideas of S. P. Novikov and P. Grinevich.

Pei Pei (Earlham): Weak solutions and blow-up for wave equations of p-Laplacian type with super-critical sources.

This paper presents a study of a quasilinear wave equation

utt - Δpu - Δut = f(u)

in a bounded domain Ω ⊂ R³ with Dirichlét boundary conditions. The operator Δ_p, 2 < p < 3 denotes the p-Laplacian. The nonlinear feedback f(u) is a source which is allowed to have a supercritical exponent, in the sense that the associated Nemytski operator is not locally Lipschitz from $W_0^{1,p}$(Ω) into L²(Ω). The linear term Δu_t provides a damping effect. Under suitable assumptions on the parameters, we prove the existence of local weak solutions, which can be extended globally provided the damping term dominates the source in some sense. Moreover, a blow-up result is proved for solutions with negative initial total energy. Part of this study is joint work with M. A. Rammaha and D. Toundykov.

Guanying Peng (Cincinnati): Analysis of the Lawrence-Doniach model for layered superconductors in magnetic fields.

We analyze minimizers of the Lawrence-Doniach energy for layered superconductors occupying a bounded generalized cylinder. For an applied magnetic field H_ex = h_exe₃ that is perpendicular to the layers with |ln ε| ≪ h_ex ≪ ε^-2 as ε → 0, where ε is the reciprocal of the Ginzburg-Landau parameter, we prove an asymptotic formula for the minimum Lawrence-Doniach energy as ε and the interlayer distance s tend to zero. We also discuss some compactness and lower bound estimate results on minimizers of the Lawrence-Doniach energy with the magnetic field in the regime h_ex = O(|ln ε|). Part of this work is joint work with P. Bauman at Purdue University.

Carlos Pérez (UPV/EHU and Ikerbasque): On commutators of singular integral operators with BMO functions.

Commutators of singular integral operators with BMO functions were introduced in the seventies by Coifman-Rochberg and Weiss. These are very interesting operators for many reasons and their study became a classical topic in modern harmonic analysis. One reason of this interest is due to the fact that they are more singular than Calderón-Zygmund operators. This idea can be expressed in many ways. In this lecture we plan to give three reasons showing this "bad" behavior.

One of them is related to a sharp weighted L² estimate with respect to A₂ weights. The novelty is that the bound in term of the A₂ constant of the weight is quadratic and no better, while in the case of singular integrals it is simply linear. The second reason is due to the fact that there is an appropriate local sub-exponential decay, which in the case of singular integrals is of exponential type instead. The third reason is related to the fact that commutators are controlled by iterations of the maximal function with a sharp new A_∞ constant.

Pieces of the lecture are part of joint works with D. Chung and C. Pereyra, with C. Ortiz and E. Rela, with T. Luque and E. Rela and with T. Hytönen.

Guillermo Rey (Michigan State): A pointwise estimate for positive dyadic shifts and some applications.

We prove a pointwise estimate for positive dyadic shifts of complexity m which is linear in the complexity. This can be used to give a pointwise estimate for Calderón-Zygmund operators and to answer a question posed by A. Lerner. Several applications to weighted estimates for both multilinear Calderón-Zygmund operators and square functions are discussed.

Alexander Reznikov (Vanderbilt): Covering properties of random points.

How many gas pumps should one build to ensure that every driver has a pump at a fixed small distance? Where should one place these pumps to minimize the number? It turns out that randomly placed points cover a regular set very well (even though they may be separated very badly). We will discuss this and related results.

Jiawei Shen (Wayne State): Singular Moser-Trudinger inequality with exact growth condition on the whole hyperbolic space.

In this talk we prove the Singular Moser-Trudinger Inequality with Exact Growth condition on the whole Hyperbolic Space. Such inequalities without Exact Growth condition on bounded and unbounded domain in the Hyperbolic space were previously given by Guozhen Lu and Hanli Tang. By replacing the Dirichlet norm by the standard Sobolev norm, we can obtain a better result for the unbounded domain in the Hyperbolic space.

David Smith (Cincinnati): Heat on a network.

The recent Unified Transform Method of Fokas is a powerful tool in the study of initial-boundary value problems for integrable nonlinear evolution equations, where the spatial domain is a half-line or finite interval. Remarkably, a linearization of the method can be used to solve all such well-posed problems for linear evolution equations, and to determine well-posedness. In this talk, we detail progress towards implementing the linearized method for spatial domains made up of several intervals, with interface conditions governing the behavior at the ends. As a simple example, we study the diffusion of heat through networks of metal rods with different material properties.

Peter Sternberg (Indiana): Minimizers of a nonlocal isoperimetric problem in thin domains.

The nonlocal isoperimetric problem arises as a certain limit of the Ohta-Kawasaki model for diblock copolymers. As a variational problem, it takes the form of a competition between a local term favoring low surface area and a nonlocal term favoring high oscillation. In this talk I will survey some of the previous activity on this problem (of which there is a lot) and then focus on a result by Massimiliano Morini and me in the setting of thin domains where we can identify the global minimizer for all values of the coefficient of nonlocality.

Patrick Tolksdorf (Darmstadt): Maximal regularity for the Stokes operator in bounded Lipschitz domains.

Hong Yue (Georgia College): Nonhomogeneous weighted div-curl lemmas for the local Hardy space h¹.

We prove two versions of the div-curl lemma for the local weighted Hardy space h¹ with nonhomogeneous conditions. This is joint work with Der-Chen Chang (Georgetown University) and Galia Dafni (Concordia University)

Lu Zhang (Wayne State): L^p estimate for a trilinear pseudo-differential operator.

We study the L^p estimate for a trilinear pseudo-differential operator with flag symbols. That is, the symbols are in the form of the product of two standard symbols from the Hörmander class ${BS}_{1,0}^0$. This operator is an extension from the trilinear operator with flag singularities, with the symbols in the form of product of two Marcinkiewcz-Mikhlin-Hörmander symbols. This extends the work of C. Muscalu on L^p estimates for a trilinear operator of Fourier multipliers of flag singularity to the case of pseudo-differential operator setting. Our work is based on the use of paraproducts and some careful decay estimates. This is joint work with Guozhen Lu.

Yaowei Zhang (Kentucky): The Bourgain-spaces and recovery of magnetic and electronic potentials of Schrödinger operators.

We use semiclassical pseudodifferential operator on semiclassical Sobolev spaces and Bourgain-type spaces defined by using the symbol of the operator h²Δ + h μ · D to recover a magnetic field and electric potential in a domain in Rⁿ for n ≥ 3 from the Dirichlet to Neumann map. This problem is related to the magnetic Schrödinger operator, with the assumption that the magnetic potential is in C^{1/2+ ε} and the electric potential is in the form ∇p with p ∈ C^1/2+ε.

Xiaodan Zhou (Pittsburgh): A game-theoretic proof of convexity preserving properties for motion by curvature.

In this talk, we present new proofs of convexity preserving properties for the p-Laplace equation and the level set mean curvature flow equation by using game-theoretic approximations. Our new proofs are based on selecting appropriate game strategies and iterating the corresponding dynamic programming principles.