The final step in the processing of astronomical spectra is the conversion of the data into real physical flux density units _ energy per unit surface area per unit wavelength/frequency interval. (Note: during the past decade, most astronomers dealing with spectral energy distributions over a wide range in wavelength/frequency have adopted λF_λ or νF_ν as the quantity plotted. Ultimately, all measurements must be calibrated with respect to some source of known flux density, with Vega (α Lyr) or Sirius (α CMa) being the usual standard. For the fluxes of stars measured with BASS, we have used a 11,070 K blackbody normalized to 4.24x10^-12 W/m² at 10 microns for Sirius, and a 9,700 K blackbody normalized to 1.26x10^-12 W/m² for Vega. In addition, the fluxes of other selected stars (α Tau, α Boo, β Peg, β Gem) have been calibrated with respect to these two, and have been used as secondary standards. The flux calibration for Vega is shown in Figure 1, and this (along with that for Sirius, will be referred to as the ``BASS'' calibration.

Hays and Latham (1975) and Tüg, White, and Lockwood (1977) empirically determined the brightness of Vega at visible wavelengths. While comparing the brightness of a star to that of a calibration lamp at visible wavelengths is difficult (differences in atmospheric attenuation, differences in the way they illuminate the detector, etc.), doing it at infrared wavelengths where everything (including the sky) is glowing brightly is even more challenging.

In the earliest days of infrared astronomy, it was usual to assume the absolute infrared flux of Vega to be that of a blackbody with a temperature equal to its effective temperature (i.e. the T required to give the same emission integrated over the entire spectrum), normalized to the calibrated flux density at visible wavelengths. However, as Dreiling and Bell (1980) indicated, opacity effects in stars such as Vega will make the spectral gradient in the IR steeper than that of a blackbody of the effective temperature of the star.

For this reason, in 1981 I adopted the use of the stellar atmosphere models of Kurucz (1979) for calibrating the IR fluxes of the HAEBE stars in a paper on the spectral energy distributions of hot stars with circumstellar dust. The result was that the model atmosphere continuum flux was essentially identical to that of a 12,000 K blackbody (see Sitko 1981 for a more detailed discussion). ``Until a number of careful, independent, empirical, absolute IR fluxes for Vega are available, it would seem reasonable to calibrate IR systems using such models, which more realistically consider the physics of stellar atmospheres and are now readily accessible in the literature, than to calibrate using blackbodies'' (Sitko 1981).

The situation worsened at the time that the Infrared Astronomical Satellite (IRAS) flew. One of its instruments, the Low Resolution Spectrograph (LRS) made measurements of the IR spectra of thousands of stars. The archived data were all calibrated using Aldebaran as the flux standard, again assuming it was a blackbody. In reality, its spectrum contains an atmospheric absorption band due to SiO that causes the actual spectrum to deviate locally from a blackbody by as much as 10% Cohen et al. 1992). Thus, both continuous opacity and line opacity sources can cause a star’s spectrum to deviate from a blackbody with a temperature equal to the effective temperature of the star.

In order to remedy this situation, M. Cohen and collaborators embarked on a program to produce a network of absolute fluxes for bright stars in the infrared (of particular interest here are Cohen et al. 1995, 1996). Ultimately, these are all tied to Kurucz stellar atmosphere models. The absolute flux calibration for Vega determined in this manner is shown in Figure 1, along with my 1981 values for comparison.

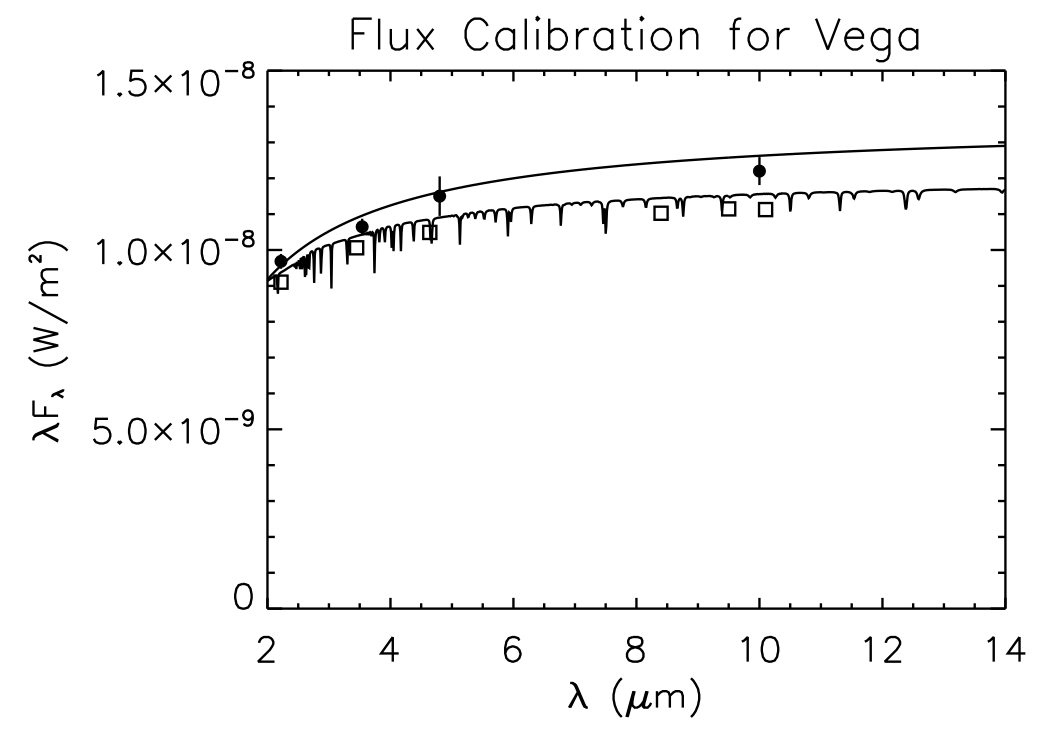
Figure 1. A comparison of the various flux calibration systems: BASS (upper curve), Cohen (lower curve), old Sitko (squares), and empirical values from Campins et al. And Rieke et al. (filled circles).

In the meantime, Campins, Rieke, and Lebofsky (1985) and Rieke, Lebofsky, and Low (1985) used a variety of techniques to empirically determine the absolute fluxes of Vega and Sirius. Their results, and the associated errors, are also shown in Figure 1. For the Campins et al. numbers, I have used the mean value they determined from both their measured values and those of Blackwell et al. (1983). For the Rieke et al. work, I have used the _direct calibration_ values from their Table I. The empirically-determined flux calibrations for Vega are all systematically higher than the model-determined ones of Cohen et al.

As can be seen in the figure, the BASS flux calibration is a few percent higher than the empirical values, while that of Cohen et al. are a few percent lower, and both are within one sigma of the measured values. For this reason, I have provided the fluxes in both systems, and you can choose whichever one you desire. The fluxes in the Cohen system were, for simplicity, calculated using a 12,510 K blackbody fit to the model atmosphere, shown in Figure 2. The atomic line absorptions in the model atmosphere only remove 0.5% or less of the flux at the spectral resolution of BASS, and can be ignored in light of the other much larger uncertainties. This was done initially to allow an analytic conversion from one system to another, but ultimately, all the data was processed (or reprocessed, in the case of older data) in both systems from the start.

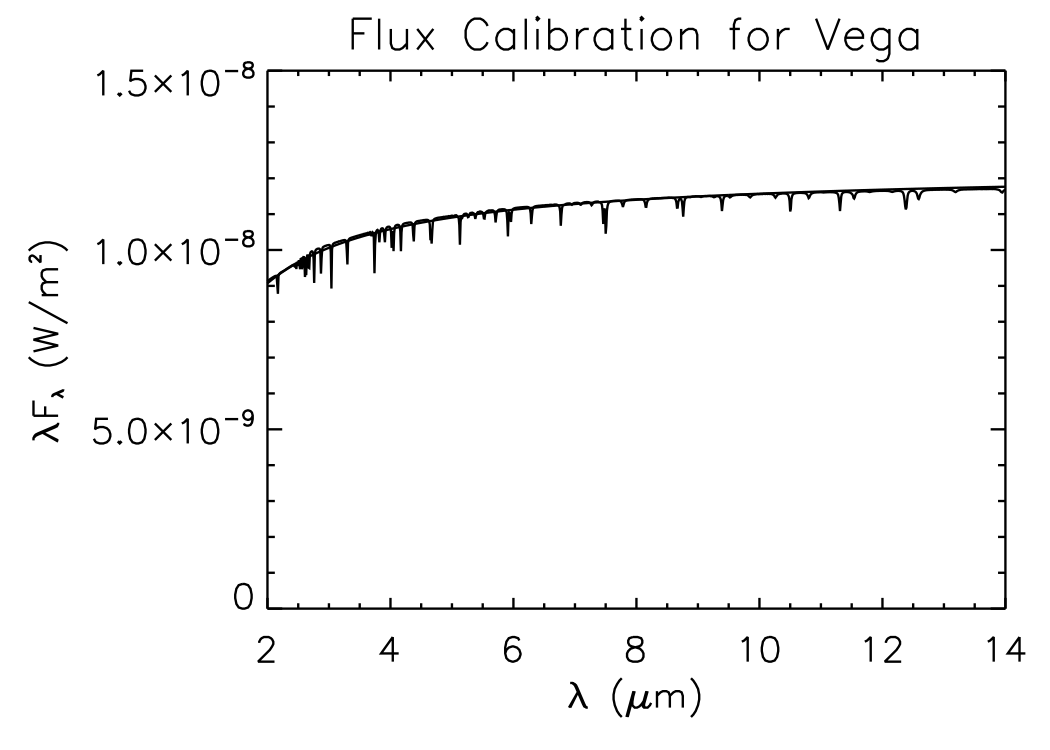
Figure 2. The Cohen model for Vega, and a T=12,600 K blackbody.

REFERENCES

Blackwell, D.E., Leggett, S.K., Petford, A.D., Mountain, C.M., and Selby, M.J. 1983, MNRAS, 205, 895

Campins, H., Rieke, G.H., and Lebofsky, M.J. 1985, AJ, 90, 896

Cohen, M., Walker, R.G., and Witteborn, F.C. 1992, AJ, 104, 2030

Cohen, M., Witteborn, F.C., Walker, R.G., Bregman, J.D., and Wooden, D.H. 1995, AJ, 110,275

Cohen, M., Witteborn, F.C., Walker, R.G., Davies, J.K., Wooden, D.H., and Bregman, J.D. 1996, AJ, 112, 2274

Dreiling, L.A. and Bell, R.A. 1980, ApJ,241,737

Hayes, D.S., and Latham, D.W. 1975, ApJ, 197, 593

Kurucz, R.L. 1979, ApJS, 40, 1

Rieke, G.H., Lebofsky, M.J., and Low, F.J. 1985, AJ, 90, 900

Sitko, M. 1981, ApJ, 247, 1024

Tüg, H., White, N.M., and Lockwood, G.W. 1977, A&A, 61, 679