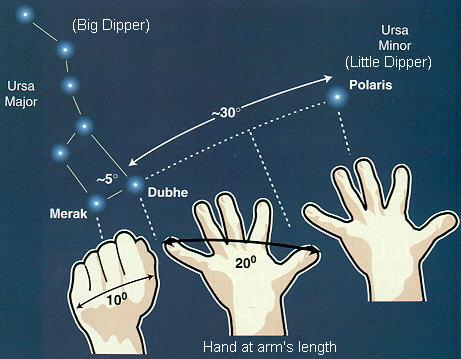
Measuring Sky Angle
One of the most important early measures handed down to the Greeks was the theory for measuring Sky Angles. We are familiar with linear distances, but in the sky we must measure angular distances. That is, relative distances on the sky (or the celestial sphere) are measured based on angles. Angles where measured in a sexagesimal (60-based) system, 60 seconds in a minute, 60 minutes in a degree, 360 degrees make up a full circle. This same system of measure, which originated thousands of years ago by the Babyonions (perhaps because they used a 360 day year), has not only survived until today, but is used in modern time keeping.
You can use your hands and fingers to measure angles in the sky. Your fingers are about 1/2o wide when you view it at arm's length. Your fist is about 10o wide. Your hand with fingers spread wide, thumb-tip to pinkie-tip subtends an angle of about 20o.