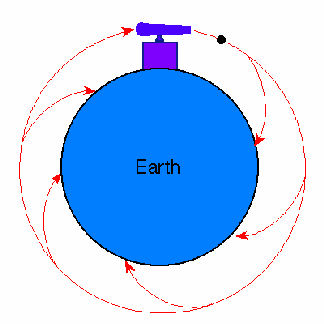
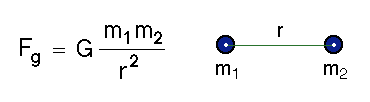Consider this thought experiment shown below. Suppose we fire a cannon horizontally from a high mountain; the projectile will eventually fall to earth, as indicated by the shortest trajectory in the figure, because of the gravitational force directed toward the center of the Earth and the associated acceleration.
An acceleration
is a change in velocity and that velocity is
a vector, so it has both a magnitude and a direction. Thus, an
acceleration occurs if either or both the
magnitude and the direction of the velocity change.
As we increase the muzzle velocity, the cannon ball will travel further before returning to earth. Newton reasoned that if the cannon ball had exactly the right velocity, it would travel completely around the Earth, always falling in the gravitational field but never reaching the Earth, which is curving away at the same rate that the projectile falls. That is, the cannon ball would have been put into orbit around the Earth. Newton concluded that the orbit of the Moon was of exactly the same nature: the Moon continuously "fell" in its path around the Earth because of the acceleration due to gravity, thus producing its orbit.
The Law of Gravity
By such reasoning, Newton came to the conclusion that
any two objects in the Universe exert gravitational attraction
on each other, with the force having a universal form.
This is Newton's Law of Gravity.
