Introduction to Imbedding Networks

Imbedding Network

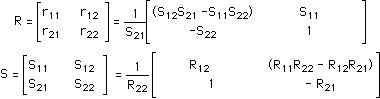
We are now going to characterize the Waveguide-Coaxial Adaptor by connecting various known impedances (a short-circuit, an open-circuit and a matched load) at one of the terminals and by making measurements through the second terminal. The known impedances connected at the first port are referred to as measurement standards.

• The waveguide-coaxial line adapter has two ports. We identify these ports with two terminal planes, (t₁ and t₂).
• The choice of the terminal planes fixes the two port parameters, If the location of these planes are moved, the resulting measurements have to be modified.
• It should also be mentioned that the results are frequency dependent and shhould be repeated at diffrent frequencies.

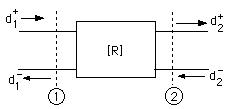
Figure shows the definition of the two port parameters for this Matrix. Here various d's represent the incident and reflected complex voltages at the corresponding ports. The now the ratios of these voltages can be mesured as corresoponding reflection coefficents at each port.

The corresponding [R] matrix can be written as:

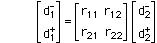
If we connect a load Z_L to Port 2, then the radio of (d₂^-/d₂⁺) will be the load reflection coefficent G_L. 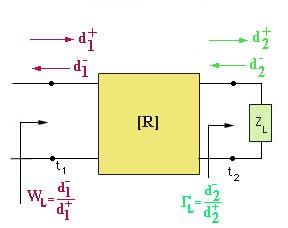With the load connected at Port 2, the reflection coefficent at Port 1 will be W_L=(d₁^-/d₁⁺).

We can expand the [R] matrix equation given above and write it as a set of two equations. If we take the ratio of the resulting equations and simplify it, we can write it as

.

If we now connect three loads with known reflection coefficients, we can measure the input reflection coefficients W_L for each G_L. This way we obtain three equations in the three unkowns (a,b and c). We can solve for the three unknowns (a,b and c). Finally, knowing these constants, we can calulate the [S] Matrix . Using the Matrix conversion equations we can determine the [Z] Matrix or [Y] Matrix , so on.

Finally the conversion equations between the [R] Matrix and [S] Matrix are given by: