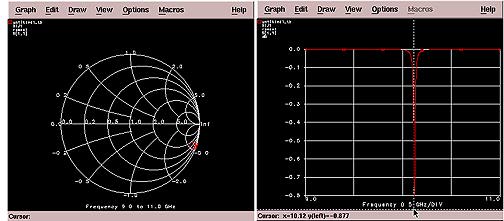
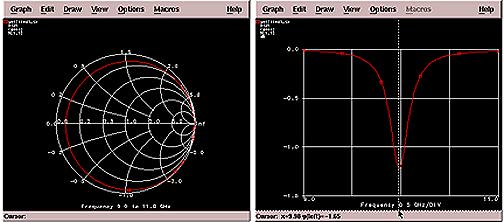
The length of the isolated resonator is l/2. The resonator is excited by a gap coupled microstrip line of characteristic impedance Z_o as shown in the figure below. The gap can be considered as a capacitor and the equivalent circuit of the resonant circuit is also shown in the figure.

The normalized input impedance can be written as

Resonance condition is obtained when the imaginary part of Z_in=0. This leads to

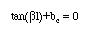
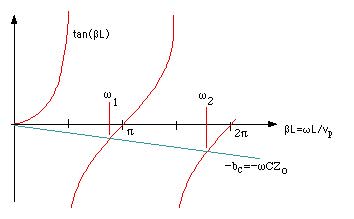
This can be solved analytically to find the resonance frequencies of the system. A graphical solution is also possible as shown in the figure below. Instead of the resonance occurring at w_o for the isolated line, the resonance is shifted to a lower frequency w₁ as shown in the figure below.

The normalized impedance in the vicinity of w₁ can be found from

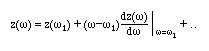
Using the given z(w)

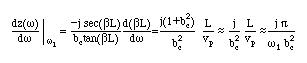
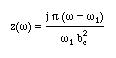
This is similar to the series resonant circuit. Even though the isolated l/2 open circuited line is equivalent to a parallel resonant circuit, the effect of the coupling capacitor has modified the resonance properties of the line.

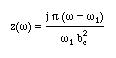
Losses can simply be included by the simple transformation and gives

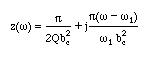
Coupling coefficient is defined for this circuit as

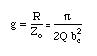
Depending on the magnitude of g, the circuit is said to be

• g=1, critical coupling.
• g>1 overcoupled
• g<1 undercoupled .

Microstrip line

• L=5.532 mm
• w=1.015 mm
• f = 10 GHz
• e_r=10
• h=1.0 mm
• t=3 mm
• tand=0.002

Gaps=1.0 mm, 0.5 mm, 0.01 mm