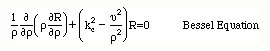
The resulting equation is given by

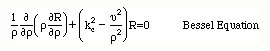
Here n is the seperation constant and k_c²=k²-b².
Since the Bessel Equation is a second order differential equation, there are two solutions. The solutions can be written as

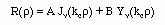
Here

• J_n(k_cr) is the Bessel function of the First kind of order n with argument k_cr.
• Y_n(k_cr) is the Bessel function of the Second kind of order n with argument k_cr.

The order n can be any number: integer and none integer. For a circular waveguide, the solutions can not be double valued. Thus, the solution should repeat at every 2p. This requires that the order n should be an integer number, i.e., n=n.

The resulting solutions can then be written as

Bessel function have properties similar to the sinusoidal functions.

The Bessel function of the first kind order (n) and argument (u) can be written as an infinite series in terms of the argument (u)

The Bessel functions of the higher order can be written in terms of the lower orders by the recursive relations

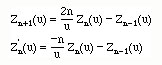
Here Z_n(u) represents either the first kind or the second kind. And the prime (') represents the derivative of the corresponding BEssel function with respect the argument (u).

The integrals of the Bessel functions also exist. As an example, the following integral equation can be derived using the properties of the Bessel functions.

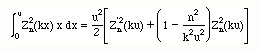
Figure below show the plot of the Bessel functions of the first and second kinds as a function of the argument (u) for the 0'th, 1'st and 2'nd orders.

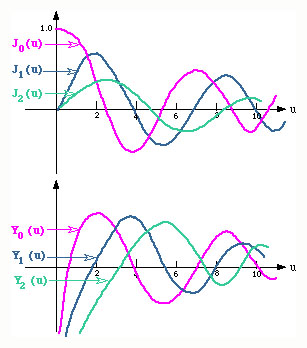
Note that all the Bessel function of the second kind have a singularity at u=0. i.e., they all go to (oo) at u=0. Since in a circular waveguide, the center of the waveguide (r=0) is included in the solution of the problem, the fields can not be infinite at the center of the waveguide. Therefore, we have to set B in the solution above equal to zero. Thus the Bessel function of the second kind is eliminated for a circular waveguide.

As can be seen from the figures for the Bessel functions figure, as the argument of the variuos Bessel functions increases, the Bessel functions go through variuos zeros.

TM Modes in a circular waveguide.

Since the E_z(r,f) is the tangential component at r=a (a=radius of the cylinder), the following equation should be satisfied.

Therefore, for this equation to be satisfied, the values of k_c times the radius (a) should be equal to the zeros of the Bessel function.

We label the zeros of the Bessel function as p_nl where n is the order of the Bessel function and l is the l'th zero of the corresponding Bessel function.

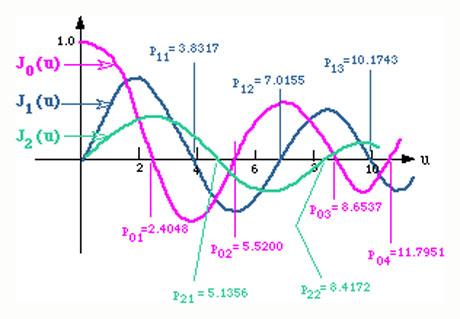
Figure below shows the corresponding zeros of the Bessel functions of the first kind.

TE Modes in a circular waveguide.

The electric field can be derived from H_z(r,f), by taking the derivative of H_z(r,f) with respect to the argument (k_cr). This leads to the boundary condition

Here the prime (') represents the derivative of the corresponding Bessel function with respect the argument (k_cr). Therefore, the values of k_c times the radius (a) should be equal to the zeros of the derivative of the Bessel function.

The zeros of the derivatives of the various Bessel functions are shown below.

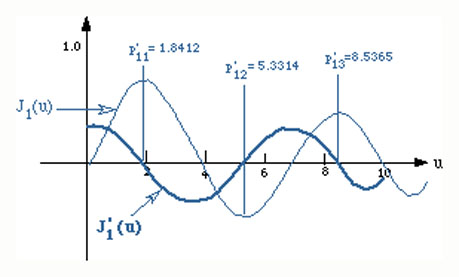
For summary the above two figures are combined into one figure as shown below in order to display the various zeros for the TE and TM modes.

The zeros of the Bessel functions and their derivatives are summarized in the tables below.

Zeros of Bessel Function (for TM modes)

n \ l	1	2	3	4
0	2.4048	5.5200	8.6537	11.7951
1	3.8317	7.0155	10.1743
2	5.1356	8.4172

Zeros of Derivatives of Bessel Functions (for TE modes)

n \ l	1	2	3	4
0	3.8317	7.0156	10.1735	13.3237
1	1.8412	5.3314	8.5363
2	3.0542	6.70061

Note the lowest zero is p'₁₁. This implies that the TE₁₁ is the lowest ordr mode that can propogate in a circular waveguide. The next mode is TM₀₁ mode. TE₁₁ is the dominant mode for the circular waveguide.