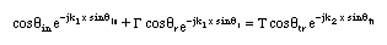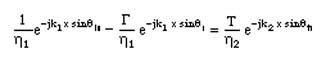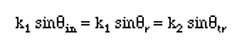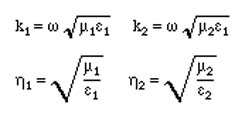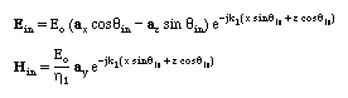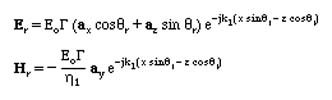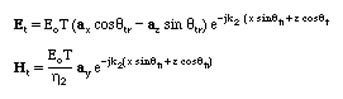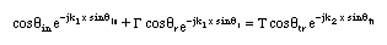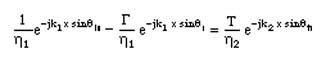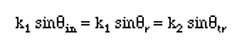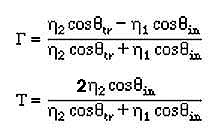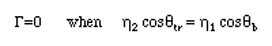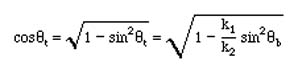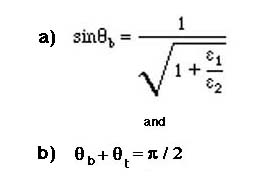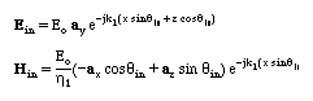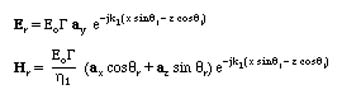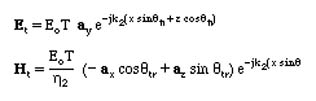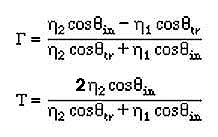University of Cincinnati--ECE&CS Department
Oblique Incidence of a Plane Wave on a Dielectric Interface
Prepared by: Prof.Altan M. Ferendeci
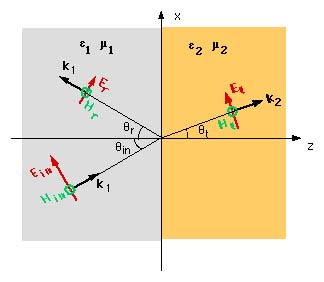
A plane wave is incident on a dieletric interface located at z=0 as shown in Figure below. The plane made by the unit normal to the interface and the propogation vector of the incoming wave is known as the plane of incidence. Depending on the direction of the E field with respect to the plane of incidence, two different solutions can be found for the reflection problem.
- E in the plane of incidence
- E perpendicular to the plane of incidence
Electric Field in the Plane of Incidence
For this case, the incident E field lies in the plane of incidence. The angle of incidence is qin, the wave is reflected at an angle of qr and the transmitted angle is qt
.
The parameters for the two regions can be written as
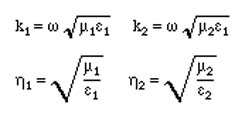
By inspection, we can write the Incident Wave as
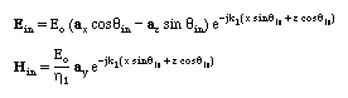
Assuming the direction of the reflected waves as shown in the figure, Reflected Wave is written by inspection as, (Here G= Reflection Coefficient)
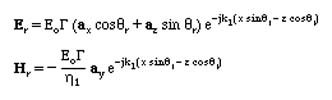
Also the Transmitted Wave is (Here T= Transmission Coefficient)
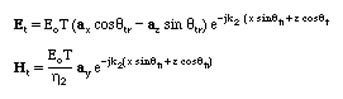
The unknowns are G and T. To solve for them, we apply the Boundary Conditions on the total fields in the two regions at the Boundary (z=0).
From the Continuity of Etangential at z=0
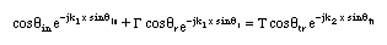
And from the Continuity of total Htangential at z=0
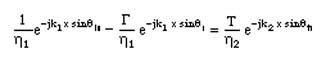
These two equation should hold for any x location.This called the constant phase assumption. Thus
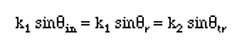
This equation yields

Results can be summarized as:
- The first equation tells us that the reflection angle is equal to the incident angle. This is called Law of Reflection.
- The second equation gives the difracted angle of the wave into the second region relative to the incident angle. This is called the Snell's Law, also known as the Law of Refraction.
Solving for the G and T, we obtain
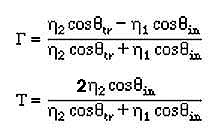
Internal Reflection
Assume that the two media are such that the e1 greater than e2. From Snell's law it apparent that qt is greater than qin. As we increase the incident angle, the refledted angle increases accordingly. The maximum qt can be equal to 90o. Beyond this, there will not be any transmitted wave, and all the incident wave will be reflected at the interface into region one. This acn be seen in the figure below.
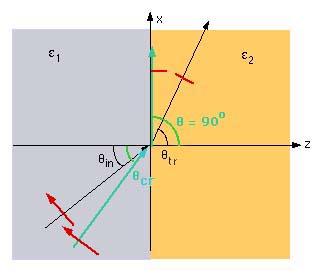
Fom Snell's law

setting qtr=90o, the critial angle is

This angle is known as the angle for critiacl reflection beyond which complete internal reflection of the wave occurs.
Brewster Angle
From the equation for G, the reflection coefficient can be zero provided the numerator of G is zero. Substituting the Snell's Law into the numerator, we can calculate the incident angle when the reflection coefficent becomes zero. For this, we set the incident angle to qin=qb
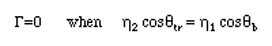
Using trigonemetric identities
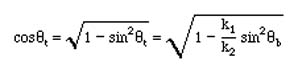
and the Snell's law, the solutions for qb becomes
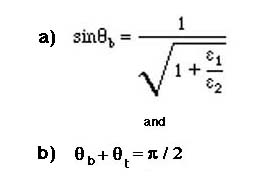
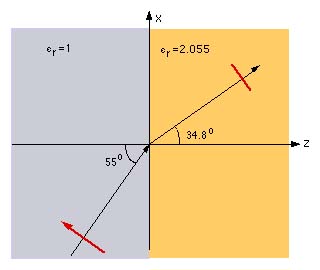
This angle is called the Brewster Angle. It is Wiedly used in optics. If a wave eith the E field in the palne of incidence is incedent on such an interfcae, the wave is totally transmitted and none is reflected.
The animation Brewster shows the Brewster angle.
E perpendicular to the plane of incidence
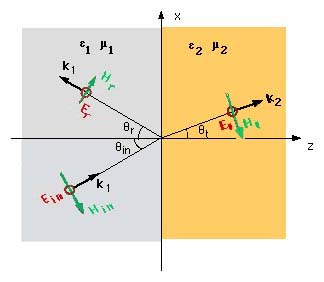
Similar field componenets can be written for an E field perpendicular to the Plane of Incidence. In this case the E field in the three cases lie in the y direction.
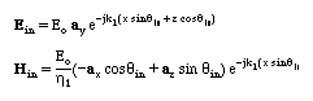
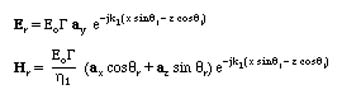
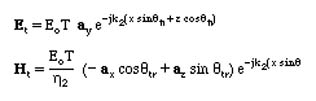
Applying the constant phase condition gives the same Law of Reflection and the Snell's Law as above. The solution to the reflection and transmission coeffients are found from the Boundary conditions as:
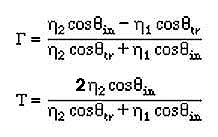
Back to Fileds I