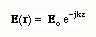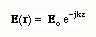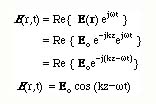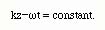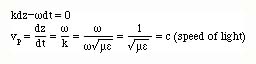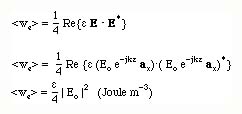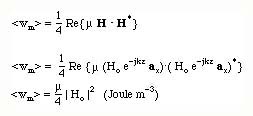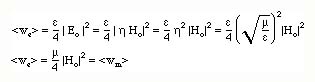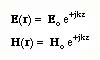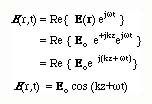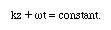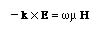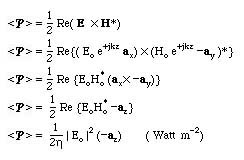Properties of Plane Waves
The electric field obtained from the solution of the Homogeneous Helmholz'z equation is given by
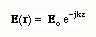
To find the actual E(r,t), we write down
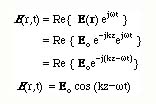
If we follow a fixed phase point of the wave, this implies that
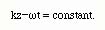
We know that time is always a positive quantity and is an increasing function.In order to satisfy the above equation, the z variable should increase in the positive z direction in order to be equal to the same constant in the equation.
If the distance increases with incrasing time, the wave should be moving with a certain velocity. Differentiating both sides of the above equations, we find
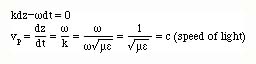
This is the velocity with which the wave moves and is known as the phase velocity of the wave. It is equal to the speed of light in a given medium. For free space it is equal to c=3x108 m/s.
Animated Wave motion Note in this animated motion, only one and a half period of tha wave is shown. In reality, for a plane wave, the wave extends from minus infinity to plus infinity.
We can also observe the wave at a given time (say t=0) and at that instant look at the wave amplitude variation as a function of position.
Wave frozen in time motion
or we can also observe the wave at a given position in space (say z=0) and at that position observe the wave amplitude variation as a function of time.
Wave frozen in space
We now calculate the average power density of the plane wave. Using the definition of the time average of Poynting Vector, we can write:

If the power density is known, the magnitude of the resulting Eo can be calulated.
We can also calculate the time averaged Electric Field Energy Density. This is:
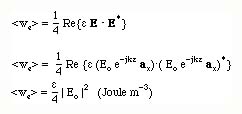
In a similar way, the Magnetic Energy density is:
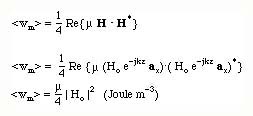
IF we substitute the magnitide relation between Eo and Ho, we obtain
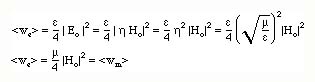
This show that the elctric and magnetiic energy densities are the same for th plane wave or they both carry the same energy density
Negatively Travelling Wave:
The solution of the wave equation resulted in two solution. So far we have considered the first term of the solution with the negative exponent
e-jk.r. We now take the seocnd solution with the positive exponent ejk.r. The E and H fields can now be written as
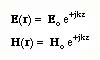
The time dependent E(r,t) field is
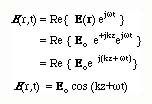
Again for constant phase, we can write
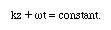
To maintain the constant phase, as the time t increases, sapce coordinate z should increase in the negative z direction (-z). This implies that the wave is a negatively travelling wave.
The relation between E, H and k is again obtained from the Maxwell's equations and is equal to
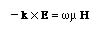
The Power density is
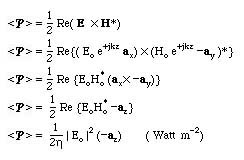
This shows that the wave is propogated in the -z direction.