University of Cincinnati--ECECS Department
Introduction to EM Fields
Prepared by: Prof.Altan M. Ferendeci

Poynting Vector

Poynting vector is a very useful quantity with which we can calculate the power flow density at a point in any space where electromagnetic fields exist.

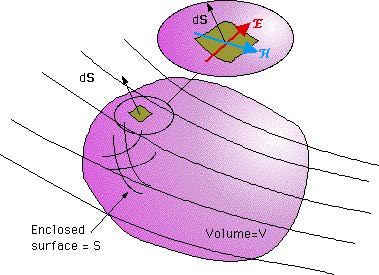
Assume that there are electromagnetic fields within and in the vicinity of a volume element V bounded by a closed surface S as shown in the figure below.

If we take the divergence of the vector product of and 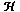, we can expend the given equation using the associated vector equality as

Substituting the corresponding curl equations for the and fields, we can write

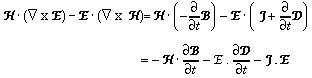
Finally

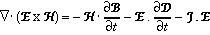
Taking the volume integral of both sides over any arbitrary volume V, the above equation can be written as

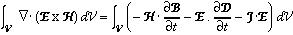
Using the divergence theorem, the left hand side can be written as

Using the constitutive relations

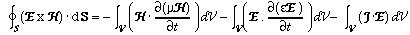
Manipulating the right hand sides of the equation, we can write it as

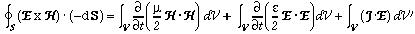
The left hand side of this equation has the units of

(Volt/m)(Amp/m)m2 = watts.

In this expression, if the the following definitions are used:

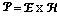
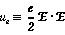
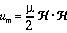
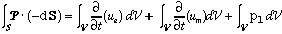
The above equation can then be written as

This equation can be thought of as the energy conservation equation for the Electromagnetic Fields.

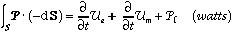
The net power flow in and out of a volume element is equal to the change in electric and magnetic energy storage and the power lost (dissipated) within the volume element V. If there is no power loss within the volume and there is no change in the electric and magnetic energy stored per unit time, then the power flow in and out of the volume element is equal.


Example: A short length of a waveguide that has negligible losses. At the same time, there are no possible changes in the field components as the fields propagate within the waveguide. Thus, the electric and magnetic energies within the volume of the waveguide will be not change. Therefore, power will be conserved. That is, whatever power enters the waveguide, it will exit from the other end without any loss..