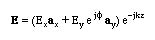
Classification of Polarization
for
Plane Waves

The Plane wave is assumed to propagate in the (+z) direction. The E and H fields lie in the (x,y) plane. It is understood that for each component of the E field in the (x,y) plane, there is an associated H field component. Therefore, in the explanation of the Plane Wave Polarization concept, H field is assumed to have similar properties as the E field.

An electric field of a plane wave can be written in general as

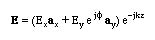
Here the angle f is an arbitrary phase angle between the x and y components of the electric field.

As a result of this equation, three basic polarization can be defined:

• Linear Polarization:

  In this case

  
  

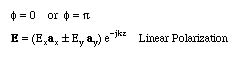
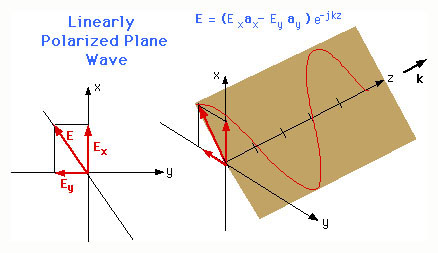
  The direction of the E field does not change. The animation Linear Polarization shows a plane polarized wave such that E=(E_xa_x-E_ya_y)e^-jkz

• Circular polarization:

  In this case

  

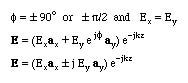
  The field rotates in a circular pattern at a frequency of w radians/sec. Looking in the direction of propogation, the field rotation is either right circularly polarized or left circularly polarized. The animation Circular Polarization shows a left circular polarized plane wave.

• Elliptic polarization:

  In this case

  

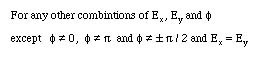
  Any combination of the E_x, E_y and f with the exception of the above conditions produces an elliptically polarized wave.
  Looking in the direction of propogation, the field rotation is either right elliptically polarized or left elliptically polarized. The animation Eliptic Polarization shows a right eliptically polarized plane wave.