University of Cincinnati--ECE&CS Department
Properties of Plane Waves in Free Spaces
Prepared by: Prof.Altan M. Ferendeci
To solve for the electromagnetic fields in a source free region, set J and r to zero in Maxweel's equations.
We start with the following equations
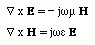Taking the curl of both sides of the first eqation
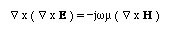and using the vector identity
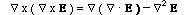
We can simplify the above equation as
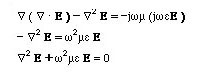Here
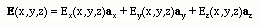If we had started with the second Maxwell's equation above and proceeded in a similar way, we would have obtained exactly the same equation for the H field.
In summary both E and H Fields satisfy
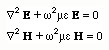These equations are called Homogeneous Helmholz's Wave Equations.
Note that each componenet of the H and E fields satsify the same equation. We can noow solve for one of the components of these fields and generalize the resulting solution for the other field components.
Initially, we take only the x component of E field, i.e. Ex(x,y,z) and look for the solutions of Ex.
We now look for a solution for the Ex field. Can we find a solution such that Ex field can be written as a product of only functions which are functions of the respective variables x, y and z? That is, can we find a solution that satisfies
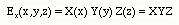
We substitute this new function into the wave equations. The result is
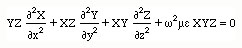Dividing both sides of the equation by XYZ, we obtain
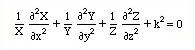Here k2=w2me. Since the last term of the equation is a constant, the other terms should also be equal to constants to satisfy the addition of functions with the same units. We set each differential term to a constant.
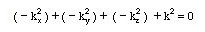Each function reduces to a simple second order differential equaition. The solution too each function can be writen as
The final solution to Ex is obtained by taking the product of these functions.
In order to simplify the analysis for the resulting solution, we keep only the first terms of the solutions and write Ex(x,y,z) as
Since the Ey and Ez components of E satisfy the same Helmholz's equation, the solution for these components are similar with the exception of the inntegration constants. Combining all there components, the E field can be written as
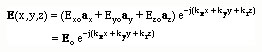If we define a propogation vector k and a position vestor r
The E field can be written simply as
Simlar result can be written directly for the H field
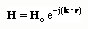
Next, we look for a relation between the E field and the H field. For this, we substitute both field solutions into the first Maxwell's eauation
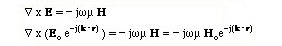Using the vector identity
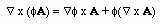and identifying the scalar and the vector quantities as
Each term in the equation reduces to
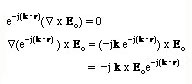
Setting this to the right hand side of the Maxwell's eqaution, we obtain
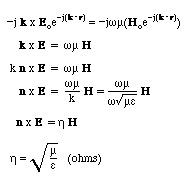
here n is a unit vector in the k direction. The constant h is known as the Wave Impedance and has the units of (Ohms). The eqation above tells us that the H field is perpendicular to th plane of the vectors k and E.
To find arelation between the k and E, we sue the Maxwell's divergence equation on E field. Substituting the E field (remember that r=0)
Using the vector identity
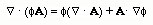
Simplifying the results, one obtains
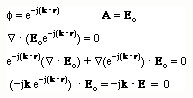
This result tells us that k and E are perpendicular to each other.
We have also shown above that H is perpendicular to the plane of k and E. Therefore, for a plane wave,
k, E and H
are all perpendicular to each other.
These can be seen in the diagram assuming that the fields propogate in the z direction.
To see a larger picture click on the diagram.
Constant Phase Front
The phase term in the exponential (k.r) can be taken equal to a constant. Assume that the wave propogation vector k is in an arbitrary direction. Any position vector r whose projection on the k vector (because of k.r is a scalar product) is constant will give the same phase value. Such a constant phase is a plane perpendicular to the direction of propogation and it is called the constant phase plane.
These are the basic properties of the plain waves.
)
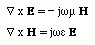
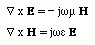
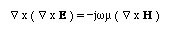
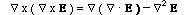
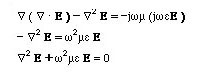
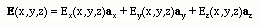
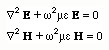
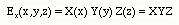
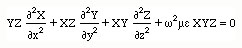
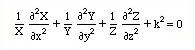
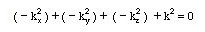
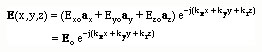
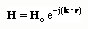
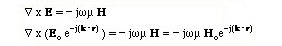
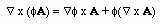
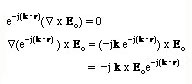
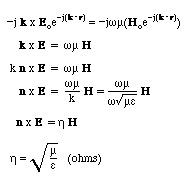
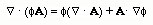
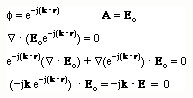
To see a larger picture click on the diagram.