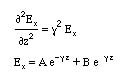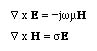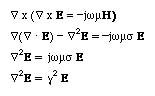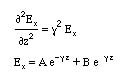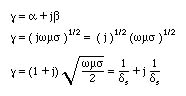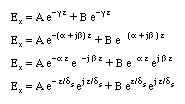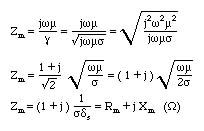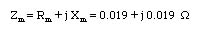University of Cincinnati--ECE&CS Department
Properties of Plain Waves in a Good Conductor (Metal)
Prepared by: Prof.Altan M. Ferendeci
For a good conductor, Maxwell's equationa can be written as
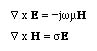
We first take the curl of both sides of the first equation. We then substitute the vector identity (curl curl of vector) and the second Maxwell's equation into the first equation, we obtain:
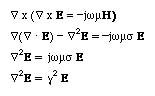
A similar equation can be obtained for the H field.
We look for the solution of this equation by assuming that there is only z dependent variation for the fields. The wave equation in a good conductor can then be written as
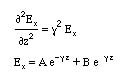
Here g is the propogation constant and is a complex quantity and is defined as g2=jwms. Defining the real part as a and the imaginary part as b, we find for the complex propogation constant
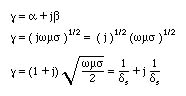
Here ds is called the skin depth and is function of frequency.
Skin depth ds for Gold is 0.67 mm at 10 GHz. At microwave frequecies and in a good conductors, the fields decay over very short distances.
.
Substituting g into the solution for E field, we can write
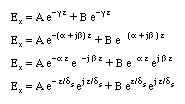
Note that the fields are attenuated with an attenuation constant of ds. For the second term, the z is increaing in the negative direction. Therefore, the same attenuation still holds for the negatively travelling wave.
To find the relation bewtween the E and H fields, we use the first Maxwells's equation above. Substituting the E field and manipulating the resulting equation we find

This results can be interperated as follows:
- The E and H are still perpendicular to each other.
- The wave impedance is given by Zm is given by
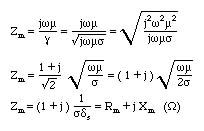
and is a compleax quantity which has equal real and imaginary parts. Calculating the wave impedance for Copper at 10 GHz, we find
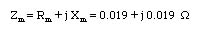
Thus the wave impedance is a very small quantity compared to the free space wave impedance and decreses further with increasing conductivity. for s=oo (perfect conductor), the wave impedance becomes zere.
Back to Micro. Comm.