Complex Numbers

Real numbers are numbers that we deal with in everyday life. Complex numbers are not real numbers but were introduced to manipulate time harmonic electrical systems. It is in a sense still the representation of real phenomenon in a way to manipulate and simplify this representation.

The building block for complex numbers is . (Physicists use i in place of j).

A complex number is represented by:

c=a+jb

Here a is the real part of c (Re(c)) and jb is the imaginary part of c (Im(c)).

The complex number c is represented on a two dimentional plane as a point as shown in the Figure below.

The Abscissa is the Real-axis and the Ordinate is the Imaginary-axis. The projection of c on the real axis is a and the projection of c on the Imaginary axis is jb

The complex number c can also be written as

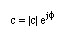
Here |c| is the Magnitude of c and f is the Phase-angle of c with respect to the Real axis.

Complex Conjugate of a complex number is defined as

c*=(a+jb)*=a-jb

Here the imaginary part is replaced by it's negative.

We can add two complex numbers:

The real and imaginary parts of the two complex numbers are added.

Example: Given:
c=a+jb
d=e-jf
z=c+d = (a+jb) + (e-jf) = (a+e) +j(b+(-f))= (a+e) + j(b-f)

We can subtract two complex numbers:

The real and imaginary parts of the two complex numbers are subtracted.

Example: Given:
c=a+jb
d=e-jf
w=c-d = (a+jb) - (e-jf) = (a-e) + j(b+f)

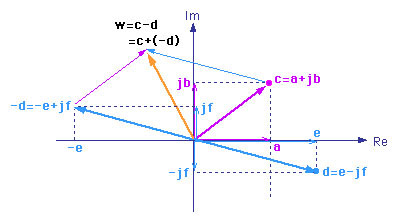
This can also be thought of: adding to c, the negative of (d)

As can be seen from the figures above, complex numbers can also be represented as vector quantities similar to two dimensional vectors. Their addition and subtraction follow similar vector addition and subtraction rules.

Multiplication of two complex numbers:

Given:
c=a+jb
d=e+jf
w= cd =(a+jb)(e+jf) = ae +jaf +jbe + (jb)(jf) = ae +jaf +jbe + j²(bf) = (ae-bf)+j(af+be)

Here j²=-1 is used.

Division of two complex numbers can be writen as

Given:
c=a+jb
d=e+jf

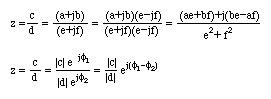
The numerator and the denominator are multiplied by the complex conjugate of the denominator, both denominator and the numerator are then multiplied using the rules for complex number multiplication and the real and imaginary parts are seperated.

The multiplication can also be carried out using the magnitudes and the phase angles. The magnitide of the numrator |c| is divided by the magnitude of the denomintor |d| and the phase angle of the denominator f₂ is subtracted from the phase angle of the numerator f₁.

Goto Homepage