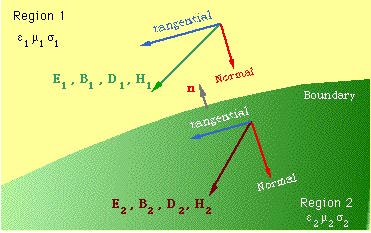
The changes in the field components from one medium to the other should be known. But these changes, that is the waves reflected and transmitted, should be consistent with Maxwell's equations.
Figure below shows two media seperated by a boundary.

Let
Tangential Component of EThe following Boundary conditions can be summarized to the special cases:: Tangential Component of E field is Continuous
Tangential Component of H
: Tangential Component of H field changes by the Infintitesimal Current density Js if present at the boundary
Normal Component of D
: Normal Component of D field changes by the surface current density ss if present at the boundary
Normal Component of B
: Normal Component of B field is continuous at the boundary
| Boundary Conditions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Field Components | General Conditions | Dielectric Boundary | Perfect Conductor | ||||||||
 |
 |
 |
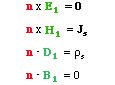 |
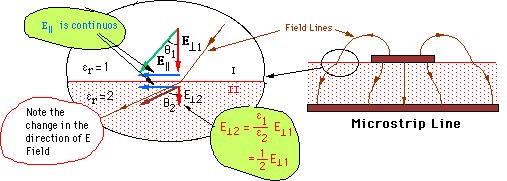
Examples:
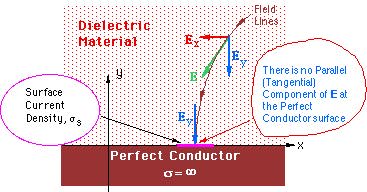
Note
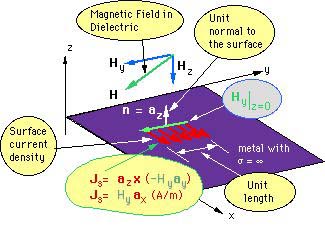
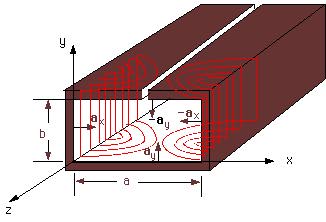
A rectangular Waveguide with inner dimensions (a,b) (y=0 to b and x=0 to a) is shown in the figure.The magnetic field for the TE10 mode is given by
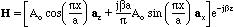
We can find the current density on the inner conductor walls from

The current density at x=0 as a function of y is calculated from
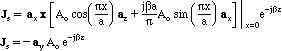
Note that the current density is constant on this wall.
The current density at x=a for any y is calculated from

Note that the current density is also constant on this wall.
The current density at y=0 as a function of x is calculated from
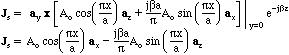
The current density at y=b as a function of x is calculated from
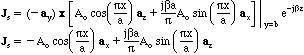
The current density is plotted in the figure for half a wavelength along the z-direction and it repeats itself along the z-axis. Note that the curent density (therefore, the current) is zero at x=a/2 both at the upper and lower walls. A slot opened at this position along the z-axis will not alter the field pattern as well as the current flow on the waveguide. A slot on the upper or lower walls may be used to insert a probe into the waveguide to monitor the strength of the propogating fields as well as the standing wave ratio on a line.