ECECS 349

Measurements Lab

Supplementary Notes

Accurate Measurements with an oscilloscope.

An oscilloscope usually has an equivalent input impedance of 1 MW resistance in parallel with a capacitance of 10-20 pF. This high impedance is acceptable for DC measurements since the effects of the capacitance can be neglected and the high input resistance does not load the circuit to be measured provided that voltage across a circuit to be measured has low output resistance. On the other hand for transient circuits and a high frequency circuits, the input impedance of the probe plays a very important role and should be properly compensated for accurate measurements.

Figure 1 below shows the schematic representation of the input impedance of an oscilloscope. Resistance R_sc is in parallel with a small capacitor C_sc. In general, in order to measure a voltage across the output terminals of a circuit, a coaxial cable is used to connect the scope to this circuit. Unfortunately, the coaxial cable introduces depending on the length of the cable, introduces relatively a large capacitance in parallel with the scope impedance which degrades the shape of the measured voltage further. In order to eliminate the effects the scope plus the cable impedance, a compensation circuit has to be introduced at the input of the coaxial line in series with the inner central conductor of the coaxial cable. The coaxial line with the compensation circuit is referred to as an “oscilloscope probe.”

Figure 1

The equivalent circuit of the complete measuring system is shown in Figure 1. The input of the scope is represented by R_sc in parallel with C_sc. The coaxial line is approximated by the capacitance by C_cable. The probe is represented by a resistance R_p in parallel with a capacitance C_p. The equivalent circuit is simplified as shown in Figure 2.

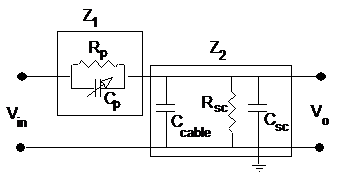
Figure 2. Simplified circuit.

Figure 2 is further simplified as shown in Figure 3 where notations for the resistors and capacitors have been simplified

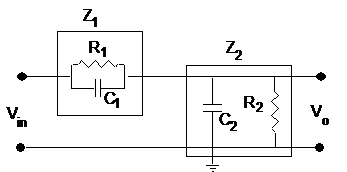
Figure 3. Further simplification of the circuit.

Here: R₁=R_p, C₁=C_p, R₂=R_sc and C₂=C_sc+C_cable.

As can be seen from Figure 3 that the circuit is a simple voltage divided and the voltage V_o at the input of the scope can be writes as

(Eq.1)

Here Z₁ and Z₂ are given by

Substituting these into Eq.1,

(Eq.2)

If we choose R₁ and C₁ as:

Substituting these back into Eq. 2

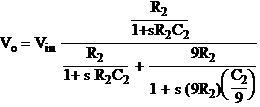
Simplifying this equation, we obtain

Note that the result is equivalent to a simple voltage divider with two resistors in series with an output voltage at the input of the scope 1/10’th of the voltage applied to the probe tips. This is the 10X setting and independent of frequency (no s-dependence).

What would be the values of R₁ and C₁ if the probe were set at 1X setting?