Robust Hypothesis Testing via Lq-Likelihood
Yichen Qin and Carey E. Priebe

Abstract:
In this article, we introduce a robust testing procedure --- the Lq-Likelihood Ratio test (LqLR) --- and show that, for the special case of testing the location parameter of a symmetric distribution in the presence of gross error contamination, our test dominates the Wilcoxon-Mann-Whitney test at all levels of contamination.


Keywords: Lq-likelihood, relative efficiency, robustness, hypothesis testing.


Our Test:
Given a data set following a distribution , in order to test the hypotheses , we propose our Lq-likelihood ratio (LqLR) test statistic to be

,

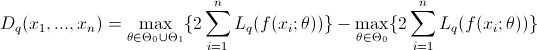where with q<1.  In the article, we have proved the robustness properties of the proposed LqLR test statistic via analysis of the asymptotic distribution.  By adaptively selecting q via the methodology described in the paper, the LqLR test provides protection of the power and size when gross error contamination is brought into the data.


Our Main Results:
Suppose we want to test the hypotheses .  We conduct the following experiment to show the advantage of the LqLR.  With the sample size of n=50, we simulate data from a gross error model where is a normal distribution with mean , the first component in h(x) is our "idealized" model, the second component in h(x) is the comtamination. 

At different levels of contamination , we first set to 0, and then generate data sets 3000 times to calculate the sizes of the tests for: (1) the Lq-likelihood ratio test (LqLR), (2) the t test i.e., the log-likelihood ratio, (3) the Wilcoxon test, and (4) the sign test.  We further change to 0.34 and repeat the previous procedure to calculate the powers for these tests.  The resutls are displayed in the following figure.


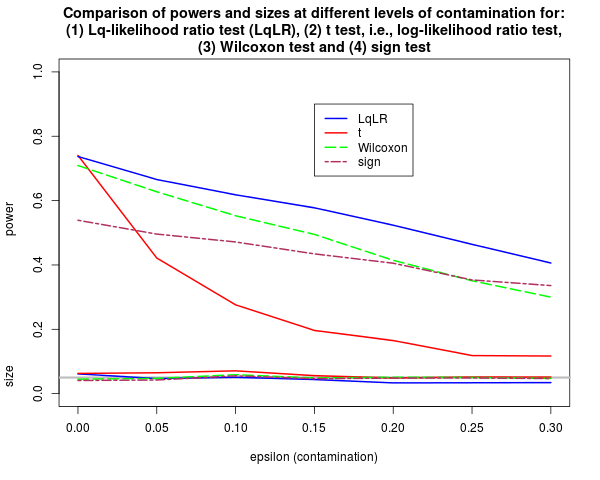
First note that the sizes of all tests are successfully controlled at 0.05.

At zero contamination (i.e., = 0), the t test (log-likelihood ratio) has the highest power. The LqLR has almost the same power (only slightly less than the t test).  The Wilcoxon and the sign tests have the third and the fourth highest powers, but not comparable to the two likelihood ratio tests.  As the contamination becomes more serious (i.e., increases away 0), the t test degrades the fastest.  Its power quickly drops below all other tests.  The Wilcoxon test and the sign test both show good robustness and their powers degrade at much slower rates.  However, the LqLR shows a remarkable robustness.  It degrades slower than the Wilcoxon test (i.e., the blue curve is flatter than the green curve), and only slightly faster than the sign test (i.e., the blue curve is steeper than the maroon curve).  Since the power of the LqLR at = 0 is above that of the Wilcoxon test and the sign test, the power of the LqLR dominates both the Wilcoxon test and the sign test at all levels of contamination!  This implies that, not only can the LqLR preserve efficiency almost perfectly at = 0, but it also obtains robustness comparable to these nonparametric tests which are known to be very robust.  We conclude that, by losing a little bit efficiency at = 0, we have traded for great robustness at > 0.  Our LqLR can be considered as a combination of the log-likelihood ratio test (at = 0) and the nonparametric tests (at > 0).  The reason our test beats nonparametric tests uniformly is that we can control the amount of information to use by selecting q, whereas the Wilcoxon test always uses the rank information, and the sign test always uses the information about whether each data point is below or above the hypothesized mean.


Conclusions:
We have introduced a robust testing procedure --- the Lq-likelihood ratio test (LqLR) --- and demonstrated its advantage over the traditional likelihood ratio test (the t test), the Wilcoxon test, and the sign test in the context of the gross error model.

To the extent that the robustness of the Wilcoxon test (minimum asymptotic relative efficiency (ARE) of the Wilcoxon test vs the t test is 0.864) suggests that the Wilcoxon test should be the default test of choice (rather than “use Wilcoxon if there is evidence of non-normality,” the default position should be “use Wilcoxon unless there is good reason to believe the normality assumption”), these new results suggest that the LqLR test should become the new default go-to test for practitioners everywhere!


Miscellaneous:
The website is created with the help of CODECOGS.