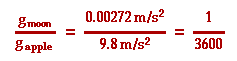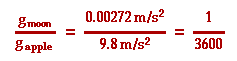Gravity and the Inverse Square Law
Newton believed the same force which causes objects on Earth to fall to
the earth also causes objects in the heavens to move along their
circular and elliptical paths. Newton's dilemma was to provide
reasonable evidence for the extension of the force of gravity from
earth to the heavens. He needed to show how the effect of gravity is
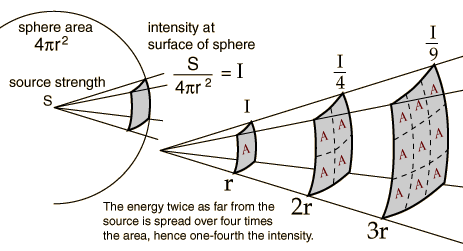
diluted with distance. It was known that the force of gravity causes
earthbound objects (such as falling apples) to accelerate towards the
earth at a rate of 9.8 m/s2. And it was also known that the moon accelerated towards the earth at a rate of 0.00272 m/s2. The force of gravity must somehow be "diluted" by distance:
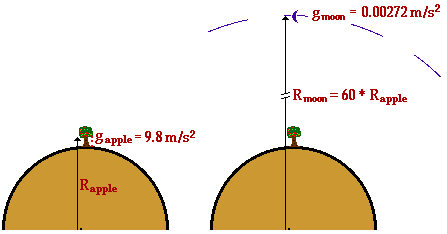The riddle is solved by a comparison between the distance from
the apple and the moon to the center of the earth. The moon is
approximately 60 times further from the earth's center than the apple
is.
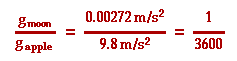The moon, being 60 times further away than the apple,
experiences a force of gravity which is 1/(60)2 = 1/3600 times that of
the apple. The force of gravity follows an inverse square law.
